First, run PERFL_2006 in one dimension. Your
PERFSTRT_2006.DAT file should look like this:
SEN90KH.ORD
NON-PARAMETRIC MULTIDIMENSIONAL UNFOLDING
1 596 10 19 1 4 20 0.025 3
(3X,9A1,7X,4A1,2X,6A1,5X,1600I1)
(I5,1X,19A1,2I5,50F8.3)
The "1" in the 3rd row is the number of dimensions. In the output file
PERF23.DAT you will find the eigenvalues of the double-centered squared distance
matrix formed from the agreement scores. Below is what these look like for the
100th Senate. The column headed by "6.1684" are the eigenvalues. Graph these in
the same fashion using Excel as you did for homework 3.
PERFORMANCE INDEX EIGENVALUE/VECTOR ROUTINE= 1 102 0 0
PERFORMANCE INDEX EIGENVALUE/VECTOR ROUTINE= 1 102 0 0
1 6.1684 50.0408 50.0408 6.3530 35.4969 35.4969
2 0.7269 5.8968 55.9376 1.1253 6.2875 41.7844
3 0.4319 3.5042 59.4418 0.6667 3.7250 45.5093
4 0.3564 2.8912 62.3330 0.4909 2.7431 48.2524
5 0.2792 2.2650 64.5980 0.4092 2.2866 50.5390
6 0.2445 1.9831 66.5812 0.3824 2.1369 52.6759
7 0.2015 1.6349 68.2160 0.3442 1.9233 54.5991
8 0.1705 1.3833 69.5994 0.3012 1.6827 56.2819
9 0.1254 1.0173 70.6166 0.2887 1.6131 57.8950
10 0.1151 0.9341 71.5507 0.2622 1.4650 59.3599
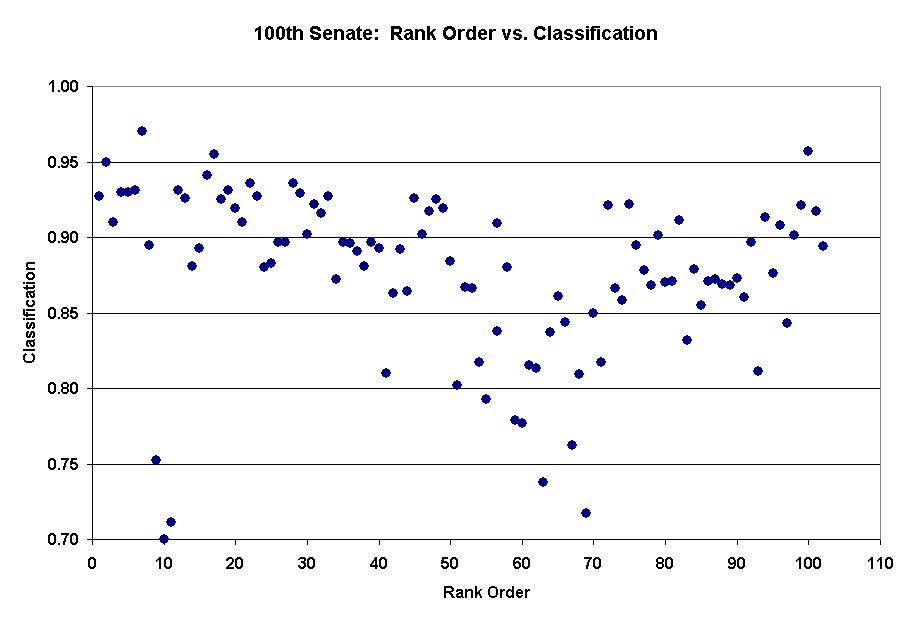
Use Excel to graph the estimated rank ordering of the Senators against the
proportion of roll call choices that are correctly classified. These are the last two
columns of PERF25.DAT (see the example in homework 3). The graph for the 100th
Senate is below. Save the one dimensional output files!