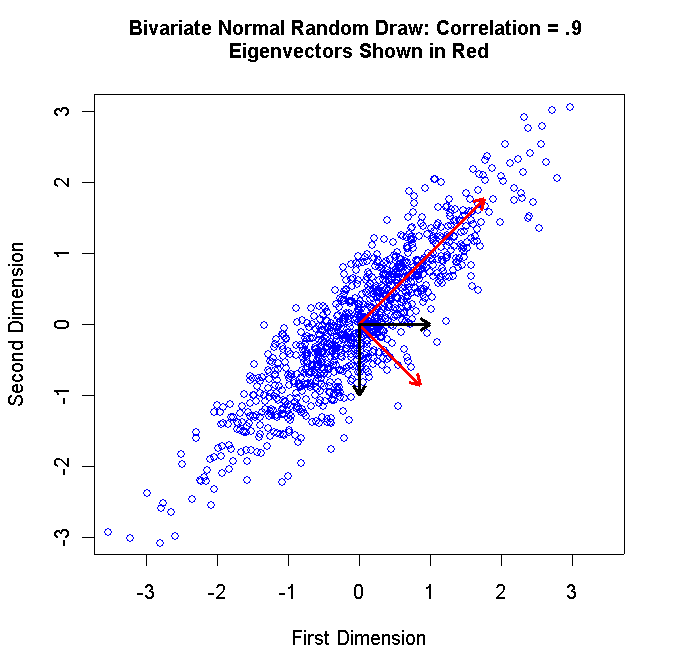
Below is a listing of the program and the graph that it creates:
#
# Program to Illustrate Singular Value Decomposition
#
# Draws n points from bivariate normal distribution
# and draws graph of points along with the
# Singular Vectors
#
nrow <- 1000
ncol <- 2
#
# Create Variance-Covariance Matrix
#
# 1.0 0.9
# 0.9 1.0
#
Sigma <- matrix(c(1,.9,.9,1),2,2)
#
# Call Bivariate Normal with zero mean and
# Sigma Var-Cov Matrix, Place in X
#
X <- mvrnorm(n=nrow,rep(0,2),Sigma)
#
# Perform Singular Value Decomposition
#
xsvd <- svd(X)
#
# The Two Lines Below Put the Singular Values in a
# Diagonal Matrix -- The first one creates an
# identity matrix and the second command puts
# the singular values on the diagonal
#
Lambda <- diag(ncol)
diag(Lambda) <- xsvd$d
#
# Compute U*LAMBDA*V' for check below
#
XX <- xsvd$u %*% Lambda %*% t(xsvd$v)
#
# Do basic plot with two line title
#
#
plot(X[,1],X[,2],asp=1,xlab="First Dimension",ylab="Second Dimension",xlim=c(-3,3),ylim=c(-3,3),col="blue")
mtext(side=3,line=1.5,"Bivariate Normal Random Draw: Correlation = .9 \nEigenvectors Shown in Red",font=2)
#
# Draw arrows for the Singular Vectors -- To make the
# plot look good, set the length of the first
# singular vector = 2.5, and the second singular
# vector = (LAMBDA_2/LAMBDA_1)*2.5. This preserves
# the ratio of the first two singular values and
# graphs the singular vectors in terms of their
# importance.
#
rat11 <- 2.5
rat22 <- (sqrt(xsvd$d[2])/sqrt(xsvd$d[1]))*rat11
sval1 <- xsvd$v[1,1]*rat11
sval2 <- xsvd$v[2,1]*rat11
arrows(0.0, 0.0,sval1,sval2,length=0.1,lwd=3,col="red")
sval1 <- xsvd$v[1,2]*rat22
sval2 <- xsvd$v[2,2]*rat22
arrows(0.0, 0.0, sval1, sval2,length=0.1,lwd=3,col="red")
#
# Rotate Matrix to its Principle Axes and Decompose it Again
#
YY <- XX %*% xsvd$v
ysvd <- svd(YY)
#
# These Two Lines draw arrows for the Singular Vectors --
# They will point along the first and second axes
#
arrows(0.0, 0.0, ysvd$v[1,1], ysvd$v[2,1],length=0.1,lwd=3,col="black")
arrows(0.0, 0.0, ysvd$v[1,2], ysvd$v[2,2],length=0.1,lwd=3,col="black")
#
#
# Compute Fit of SVD -- This is just the sum of squared
# error -- Note that ssesvd should be zero!
#
#
i <- 0
j <- 0
ssesvd <- 0
while (i < nrow) {
i <- i + 1
j <- 0
while (j < ncol) {
j <- j + 1
ssesvd <- ssesvd + (X[i,j] - XX[i,j])**2
}
}
In order for the program to run you will have to load in the MASS package. To do this click on "Packages" on the toolbar and then select "Load Package". You will get a simple drop down list. Highlight "MASS" and click "OK".
-
Reproduce the graph above and report the measure of fit -- ssesvd.
Note that your graph will not look exactly
the same since R is drawing randomly! If
the arrows do not show up well in black and white simply change
col="red" to col="black" in the arrows(...) command. You can also increase
the thickness of the arrows by increasing lwd=3 to lwd=4 or lwd=5.
Use Epsilon to change the correlation to -0.9, 0.5, and 0.0, respectively, and turn in all the graphs. Be sure that you change the titles appropriately!
For each of the above graphs, after you print out the graph, at the R prompt type:
plot(YY[,1],YY[,2],asp=1,xlab="Rotated First Dimension",ylab="Rotated Second Dimension",xlim=c(-3,3),ylim=c(-3,3),pch=16,col="blue") mtext(side=3,line=1.5,"Bivariate Normal Random Draw: Correlation = .9 \nConfiguration Rotated to Principle Axes",font=2)Turn in these graphs as well with the appropriate titles.
and place them in the same folder on a WINTEL machine. Read the Aldrich-McKelvey scaling program page to see how to run the program.
Here are the first three lines of OLS68A.DAT.
1681 0 10 1 1 1 1 1 63 4 4 5 7 1 2 2 3 7 1 1
1124 0 10 1 0 0 0 1 82 1 1 4 4 1 1 1 1 4 1 5
78 5 10 1 0 1 1 1 78 2 1 5 7 4 5 5 6 6 7 5
The variables, in order, are:
RESPONDENT ID = unique 4 digit number
PARTY ID = 0 to 6 -- 0 = Strong Democrat
1 = Weak Democrat
2 = Lean Democrat
3 = Independent
4 = Lean Republican
5 = Weak Republican
6 = Strong Republican
RAW INCOME = **do not use**
FAMILY INCOME = income quintile 1 - 5
SEX = 0 Man, 1 Woman
RACE = 0 White, 1 Black
SOUTH = 0 North, 1 South
EDUCATION = 1 High School or less, 2 Some College, 3 College
AGE = In Years
URBAN UNREST SCALE = Johnson, Humphrey, Nixon, Wallace, Self-Placement
VIETNAM SCALE = Johnson, Humphrey, Nixon, Wallace, Self-Placement
VOTED = 1 Voted, 5 Did Not Vote
-
Run the Aldrich-McKelvey scaling procedure using both the urban unrest and
vietnam files. Save the coordinate output files. Graph the scaled stimuli
coordinates against each other using R -- that is,
use the Vietnam coordinates as the horizontal axis and the Urban Unrest coordinates
as the vertical axis. Use the names of the candidates and label the graph and
the axes appropriately. Why do you think the plot looks the way it does?
Use Epsilon to merge the party ID variable from OLS68A.DAT into the coordinate output file. For example, here are the first few lines of the coordinate output file for the urban unrest scale:
LINE # CASE # R POS ALPHA BETA SCALED POS RSQ
1 1681 1.0 -2.6243 0.5249 -2.0994 0.9994 0.9997
2 1124 1.0 -0.8831 0.3532 -0.5298 0.6790 0.8240
3 78 4.0 -0.9588 0.2557 0.0639 0.8992 0.9483
4 553 4.0 -1.2302 0.2895 -0.0724 0.6460 0.8037
The second column is the respondent ID number. Use the respondent ID number
to match OLS68A.DAT with the output file and insert the party ID code into
the output file. After you have inserted the party code you can delete all the
columns except the party code, BETA (you will need that for graphing),
and the Scaled Position. If you have done everything correctly the first few
lines of your file should look like this:
0 0.5249 -2.0994
0 0.3532 -0.5298
5 0.2557 0.0639
1 0.2895 -0.0724
1 0.2763 0.6907
1 1.3930 -0.3482
0 1.0597 -0.5298
0 0.2322 -0.3482
0 0.4371 -0.8742
5 0.3901 0.6827
0 0.0033 0.0050
0 0.2119 -0.5298
1 0.2624 0.2624
2 0.2938 -0.5142
1 0.2745 0.1373
etc.
etc.
etc.
Turn in the Epsilon macro you write that inserts
the party variable into the coordinate file. In the macro, use a split
screen and place the coordinate file in the top screen and
OLS68A.DAT in the bottom screen.Read the above file into R and make smoothed histograms of the scaled positions of the respondents by party ID. To do this, read the file with the command:
T <- matrix(scan("D:/R_Files/uuheck_1.txt",0),ncol=3,byrow=TRUE)
To make a smoothed histogram of just the strong democrats:
strong.democrat <- T[T[,1]==0 & T[,2] > 0,3] This selects only the strong
Democrats with Postive Betas From
the 3rd column of T
plot(density(strong.democrat),xlab="Scaled Value Urban Unrest",main="Strong Democrat",xlim=c(-3,3),type="l",lwd=3)
This does the smoothed histogram.
Note that type="l" is "l" as in Line not
the number "1"!!!
To make a similar plot for all Democrats with Positive Betas you have to
define the variable with:
all.democrat <- T[(T[,1]==0 | T[,1]==1 | T[,1]==2) & T[,2] > 0,3]
If party is 0 or 1 or 2 AND Beta is Positive,
Select column 3
To make the smoothed histogram simply change the arguments in the plot command above.To make a smoothed histogram of both the strong Democrats and the strong Republicans use the commands:
plot(density(strong.democrat),xlab="Scaled Value Urban Unrest",main="Strong Party Identifiers",xlim=c(-3,3),type="l",lwd=3,col="red")
lines(density(strong.republican),lwd=3,col="blue") This is the trick to get
a second line in the plot!
text(1,1.3,"Red = Strong Democrats\nBlue = Strong Republicans") This puts in
a simple legend
Make smoothed histograms showing strong Democrats and strong Republicans,
all Democrats and all Republicans, Independents by themselves, and strong Democrats,
strong Republicans, and Independents. Also report the number, mean, and standard
deviation for each variable you graph (put them in a nice, neat table!!).
To get the number simply use the
"length" command; for example:ndem <- length(strong.democrat)
Recall that the commands to get the mean and standard deviation of a variable in R are simply mean(..) and sd(..), respectively.
Replicate (c) with the Vietnam Scale.
and place them in the same folder on a WINTEL machine. PERFSTRT.DAT looks like this:
SEN107KH.ORD
NON-PARAMETRIC MULTIDIMENSIONAL UNFOLDING OF 107TH SENATE
1 633 20 36 10
(36A1,3900I1)
(I5,1X,36A1,2I5,50F8.3)
The first line is the roll call data file, the second line is the title, the third
line, in order, is the number of dimensions, the number of roll calls, the
number of iterations (leave as is), the number of "characters" to read off
the front of each legislator's record (leave as is), and the record number of a
Senator that you believe is on the "Left" (this just sets "liberal" on the left --
lower ranks or negative values on the first dimension if the scaling is in
two or more dimensions -- and
"conservative" on the right). The last line is the format for
the coordinate output file.-
At the command line type
PERFL
The program should only take a few seconds to run and it produces three output files -- PERF21.DAT, PERF23.DAT, and PERF25.DAT. Turn in a copy of PERF21.DAT. It should look something like this:
21 FEBRUARY 2003 13.59.33.79.
RANDOM NUMBER SEED 116300
SEN107KH.ORD
NON-PARAMETRIC MULTIDIMENSIONAL UNFOLDING OF 107TH SENATE
1 633 20 36 10
(36A1,3900I1)
(I5,1X,36A1,2I5,50F8.3)
******************************************************************************
1 ROLL CALLS 1 4102 48745 0.08415 0.91585 0.73739
2 LEGISLATORS 1 4044 48745 0.08296 0.91704 0.74110 0.99787
3 ROLL CALLS 1 3995 48745 0.08196 0.91804 0.74424
4 LEGISLATORS 1 3981 48745 0.08167 0.91833 0.74513 0.99903
5 ROLL CALLS 1 3953 48745 0.08110 0.91890 0.74693
6 LEGISLATORS 1 3946 48745 0.08095 0.91905 0.74738 0.99922
7 ROLL CALLS 1 3935 48745 0.08073 0.91927 0.74808
8 LEGISLATORS 1 3935 48745 0.08073 0.91927 0.74808 0.99996
9 ROLL CALLS 1 3931 48745 0.08064 0.91936 0.74834
10 LEGISLATORS 1 3932 48745 0.08066 0.91934 0.74827 0.99999
13.59.33.92.
ELAPSED TIME OF JOB 13.59.36.06.
The sixth column reports the correct classification. For the 107th
Senate the algorithm quickly converges to 0.91934 (91.9%).The file PERF25.DAT contains the output coordinates for the Senators and the roll calls. In one dimension, this is reported as a rank ordering. The first part of the file shows the Senators in rank order and then in the order that they appear in the roll call file with their ranking:
21 FEBRUARY 2003 14.05.20.15.
1 1074930925 0WISCONS 10001FEINGOLD 75 498 0.849 1.000
2 1074010133 0MINNESO 10001DAYTON 19 486 0.961 2.000
3 1074010412 0NEW JER 10001CORZINE 33 495 0.933 3.000
4 1074910133 0MINNESO 10011WELLSTONE 6 484 0.988 4.000
5 1071501171 0CALIFOR 10001BOXER 23 481 0.952 5.000
6 1071303952 0MARYLAN 10001SARBANES 14 498 0.972 6.500
7 10729142 5 0RHODE I 10001REED 22 497 0.956 6.500
8 10710808 3 0MASSACH 10001KENNEDY, ED 25 480 0.948 8.000
9 1071502121 0ILLINOI 10001DURBIN 24 496 0.952 9.000
10 1071423031 0IOWA 10001HARKIN 29 488 0.941 10.000
11 10714213 1 0CONNECT 10001DODD 25 483 0.948 11.000
etc.
etc.
etc.
100 1071490853 0OKLAHOM 20001NICKLES, DO 30 495 0.939 100.000
101 1071462849 0TEXAS 20001GRAMM, PHIL 24 480 0.950 101.000
102 1071542961 0ARIZONA 20001KYL 25 495 0.949 102.000
******************************************************************************
1 1079991099 0USA 200 BUSH 2 63 0.968 70.500
2 1074970041 0ALABAMA 20001SESSIONS 54 481 0.888 65.000
3 1079465941 0ALABAMA 20001SHELBY 55 488 0.887 63.500
4 1071490781 0ALASKA 20001MURKOWSKI 26 459 0.943 70.500
5 1071210981 0ALASKA 20001STEVENS 27 452 0.940 62.000
6 1071542961 0ARIZONA 20001KYL 25 495 0.949 102.000
7 1071503961 0ARIZONA 20001MCCAIN 124 478 0.741 57.000
8 1072930642 0ARKANSA 20001HUTCHINSON, 47 484 0.903 66.000
9 1072930542 0ARKANSA 10001LINCOLN 33 495 0.933 47.000
10 1071501171 0CALIFOR 10001BOXER 23 481 0.952 5.000
etc.
etc.
Use Epsilon to combine the rank ordering
of the Senators with the W-NOMINATE coordinates
and the KYST coordinates you
estimated for Homework 3 Q.2. Read the combined
file into R and compute the correlations between
the rank ordering with the first dimension of W-NOMINATE,
the first dimension of the KYST two dimensional coordinates, and the KYST one
dimensional coordinates. Graph the rank ordering (horizontal axis) against
the first dimension of W-NOMINATE with the
appropriate titles and labels and graph the rank ordering (horizontal axis)
against the first dimension of the two-dimensional
KYST coordinates with the appropriate titles
and labels.The file PERF23.DAT has some miscellaneous diagnostics for the program including the eigenvalues of the double-centered agreement score matrix. Here is the relevant portion of the file:
etc.
etc.
PERFORMANCE INDEX EIGENVALUE/VECTOR ROUTINE= 1 102 0 0
1 9.1091 70.3239 70.3239 11.4572 57.7452 57.7452
2 0.2922 2.2557 72.5796 0.7181 3.6190 61.3642
3 0.2525 1.9493 74.5289 0.4965 2.5023 63.8665
4 0.1772 1.3683 75.8973 0.3837 1.9337 65.8002
5 0.1557 1.2019 77.0992 0.3225 1.6256 67.4258
6 0.1430 1.1040 78.2032 0.2785 1.4038 68.8296
7 0.1300 1.0040 79.2071 0.2561 1.2906 70.1203
8 0.1068 0.8245 80.0317 0.2247 1.1327 71.2530
9 0.0918 0.7090 80.7407 0.1989 1.0023 72.2553
10 0.0783 0.6041 81.3448 0.1915 0.9650 73.2203
11 0.0752 0.5806 81.9254 0.1813 0.9138 74.1341
12 0.0684 0.5280 82.4534 0.1648 0.8306 74.9647
13 0.0654 0.5049 82.9582 0.1565 0.7889 75.7537
14 0.0583 0.4503 83.4086 0.1531 0.7714 76.5251
15 0.0562 0.4336 83.8422 0.1435 0.7232 77.2483
16 0.0500 0.3857 84.2279 0.1412 0.7118 77.9600
17 0.0468 0.3614 84.5893 0.1402 0.7066 78.6667
18 0.0441 0.3405 84.9298 0.1333 0.6719 79.3385
19 0.0407 0.3146 85.2444 0.1293 0.6519 79.9904
20 0.0388 0.2999 85.5443 0.1216 0.6129 80.6032
etc.
etc.
The second column with a first entry of 9.1091 are the eigenvalues. Make
a graph of the eigenvalues like the one you did for
Homework 3 Q.2.
Use Epsilon to change the number of dimensions from 1 to 2 in PERFSTRT.DAT and run PERFL again (be sure to save the output files from the one-dimensional run first!!!! -- they will be overwritten by the new ones!). PERF21.DAT should look something like this:
21 FEBRUARY 2003 14.54.27.96.
RANDOM NUMBER SEED 87600
SEN107KH.ORD
NON-PARAMETRIC MULTIDIMENSIONAL UNFOLDING OF 107TH SENATE
2 633 20 36 10
(36A1,3900I1)
(I5,1X,36A1,2I5,50F8.3)
******************************************************************************
1 ROLL CALLS 2 3723 48745 0.07638 0.92362 0.76165 0.00000
LEGISLATORS 2 3654 48745 0.07496 0.92504 0.76607 0.00000
2 ROLL CALLS 2 3594 48745 0.07373 0.92627 0.76991 0.99244
LEGISLATORS 2 3574 48745 0.07332 0.92668 0.77119 0.99799
3 ROLL CALLS 2 3552 48745 0.07287 0.92713 0.77260 0.99702
LEGISLATORS 2 3546 48745 0.07275 0.92725 0.77298 0.99808
4 ROLL CALLS 2 3540 48745 0.07262 0.92738 0.77337 0.99653
LEGISLATORS 2 3539 48745 0.07260 0.92740 0.77343 0.99991
5 ROLL CALLS 2 3534 48745 0.07250 0.92750 0.77375 0.99849
LEGISLATORS 2 3533 48745 0.07248 0.92752 0.77382 0.99995
6 ROLL CALLS 2 3531 48745 0.07244 0.92756 0.77394 0.99821
LEGISLATORS 2 3531 48745 0.07244 0.92756 0.77394 0.99985
7 ROLL CALLS 2 3528 48745 0.07238 0.92762 0.77414 0.99989
LEGISLATORS 2 3527 48745 0.07236 0.92764 0.77420 0.99955
8 ROLL CALLS 2 3525 48745 0.07232 0.92768 0.77433 0.99918
LEGISLATORS 2 3525 48745 0.07232 0.92768 0.77433 0.99999
9 ROLL CALLS 2 3524 48745 0.07229 0.92771 0.77439 0.99882
LEGISLATORS 2 3524 48745 0.07229 0.92771 0.77439 0.99999
10 ROLL CALLS 2 3524 48745 0.07229 0.92771 0.77439 0.99867
LEGISLATORS 2 3524 48745 0.07229 0.92771 0.77439 1.00000
11 ROLL CALLS 2 3523 48745 0.07227 0.92773 0.77446 0.99994
LEGISLATORS 2 3523 48745 0.07227 0.92773 0.77446 1.00000
12 ROLL CALLS 2 3523 48745 0.07227 0.92773 0.77446 0.99910
LEGISLATORS 2 3523 48745 0.07227 0.92773 0.77446 1.00000
13 ROLL CALLS 2 3522 48745 0.07225 0.92775 0.77452 0.99808
LEGISLATORS 2 3522 48745 0.07225 0.92775 0.77452 1.00000
14 ROLL CALLS 2 3521 48745 0.07223 0.92777 0.77458 0.99778
LEGISLATORS 2 3521 48745 0.07223 0.92777 0.77458 1.00000
15 ROLL CALLS 2 3521 48745 0.07223 0.92777 0.77458 0.99715
LEGISLATORS 2 3524 48745 0.07229 0.92771 0.77439 1.00000
16 ROLL CALLS 2 3521 48745 0.07223 0.92777 0.77458 0.99721
LEGISLATORS 2 3521 48745 0.07223 0.92777 0.77458 1.00000
17 ROLL CALLS 2 3521 48745 0.07223 0.92777 0.77458 0.99768
LEGISLATORS 2 3521 48745 0.07223 0.92777 0.77458 1.00000
18 ROLL CALLS 2 3521 48745 0.07223 0.92777 0.77458 0.99691
LEGISLATORS 2 3520 48745 0.07221 0.92779 0.77465 0.99999
19 ROLL CALLS 2 3520 48745 0.07221 0.92779 0.77465 0.99727
LEGISLATORS 2 3520 48745 0.07221 0.92779 0.77465 0.99999
20 ROLL CALLS 2 3434 48745 0.07045 0.92955 0.78015 0.99401
LEGISLATORS 2 3431 48745 0.07039 0.92961 0.78035 0.99948
MEAN VOLUME LEG. 0.0047 0.0068 3.6961 6.7777 -0.0264
MACHINE PREC. 2 3430 48745 0.07037 0.92963
14.54.28.01.
ELAPSED TIME OF JOB 14.56.17.40.
The correct classification is now 92.963% (0.92963). The first few lines of
PERF25.DAT should look very similar to this:
21 FEBRUARY 2003 14.54.27.96.
1 1079991099 0USA 200 BUSH 1 63 0.984 0.063 0.208 0.280
2 1074970041 0ALABAMA 20001SESSIONS 50 481 0.896 0.002 0.224 -0.178
3 1079465941 0ALABAMA 20001SHELBY 44 488 0.910 0.007 0.181 0.200
4 1071490781 0ALASKA 20001MURKOWSKI 21 459 0.954 0.004 0.198 0.140
5 1071210981 0ALASKA 20001STEVENS 32 452 0.929 0.003 0.177 0.157
6 1071542961 0ARIZONA 20001KYL 23 495 0.954 0.002 0.285 -0.359
7 1071503961 0ARIZONA 20001MCCAIN 62 478 0.870 0.002 0.130 -0.665
8 1072930642 0ARKANSA 20001HUTCHINSON, 45 484 0.907 0.012 0.199 0.187
9 1072930542 0ARKANSA 10001LINCOLN 27 495 0.945 0.002 -0.112 0.327
10 1071501171 0CALIFOR 10001BOXER 22 481 0.954 0.012 -0.275 -0.115
The last two columns are the two-dimensional coordinates. Make a two-dimensional plot
of the coordinates using R. Use the names of the
Senators and label the axes and the plot appropriately.Make a two-dimensional plot of the 107th Senate with "D" representing non-Southern Democrats, "S" representing Southern Democrats, "R" representing Republicans, and "P" representing President Bush. You can modify my R program:
to do this. Note that you will have to add a line to the program to display the "P" for President Bush. Be sure to correctly label the graph.