The aim of this problem is to show you how to double-center a
matrix in R and extract the eigenvalues and
eigenvectors of the matrix.
Use the R program below to do this exercise:
Double_Center_Drive_Data.r -- Program to
Double-Center a Matrix of Squared Distances
#
# double_center_drive_data.r -- Double-Center Program
#
# Data Must Be Transformed to Squared Distances Below
#
# ATLANTA 0000 2340 1084 715 481 826 1519 2252 662 641 2450
# BOISE 2340 0000 2797 1789 2018 1661 891 908 2974 2480 680
# BOSTON 1084 2797 0000 976 853 1868 2008 3130 1547 443 3160
# CHICAGO 715 1789 976 0000 301 936 1017 2189 1386 696 2200
# CINCINNATI 481 2018 853 301 0000 988 1245 2292 1143 498 2330
# DALLAS 826 1661 1868 936 988 0000 797 1431 1394 1414 1720
# DENVER 1519 891 2008 1017 1245 797 0000 1189 2126 1707 1290
# LOS ANGELES 2252 908 3130 2189 2292 1431 1189 0000 2885 2754 370
# MIAMI 662 2974 1547 1386 1143 1394 2126 2885 0000 1096 3110
# WASHINGTON 641 2480 443 696 498 1414 1707 2754 1096 0000 2870
# CASBS 2450 680 3160 2200 2330 1720 1290 370 3110 2870 0000
#
# Remove all objects just to be safe
#
rm(list=ls(all=TRUE))
#
library(MASS)
library(stats)
#
#
T <- matrix(scan("C:/uga_course_homework_5_2015/drive2.txt",0),ncol=11,byrow=TRUE)
#
nrow <- length(T[,1])
ncol <- length(T[1,])
# Another way of entering names -- Note the space after the name
names <- c("Atlanta ","Boise ","Boston ","Chicago ","Cincinnati ","Dallas ","Denver ",
"Los Angeles ","Miami ","Washington ","CASBS ")
#
# pos -- a position specifier for the text. Values of 1, 2, 3 and 4,
# respectively indicate positions below, to the left of, above and
# to the right of the specified coordinates
#
namepos <- rep(2,nrow)
#
TT <- rep(0,nrow*ncol)
dim(TT) <- c(nrow,ncol)
TTT <- rep(0,nrow*ncol)
dim(TTT) <- c(nrow,ncol)
#
xrow <- NULL
xcol <- NULL
xcount <- NULL
matrixmean <- 0
matrixmean2 <- 0
#
# Transform the Matrix
#
i <- 0
while (i < nrow) {
i <- i + 1
xcount[i] <- i Ignore -- Just a diagnostic
j <- 0
while (j < ncol) {
j <- j + 1
#
# Square the Driving Distances
#
TT[i,j] <- (T[i,j]/1000)**2 Note the division by 1000 for scale purposes
#
}
}
#
# Put it Back in T
#
T <- TT
TTT <- sqrt(TT) This creates distances -- see below
#
#
# Call Double Center Routine From R Program
# cmdscale(....) in stats library
# The Input data are DISTANCES!!! Not Squared Distances!!
# Note that the R routine does not divide
# by -2.0
#
ndim <- 2
#
dcenter <- cmdscale(TTT,ndim, eig=FALSE,add=FALSE,x.ret=TRUE)
#
# returns double-center matrix as dcenter$x if x.ret=TRUE
#
# Do the Division by -2.0 Here
#
TTT <- (dcenter$x)/(-2.0) Here is the Double-Centered Matrix
#
#
# Below is the old Long Method of Double-Centering
#
# Compute Row and Column Means
#
xrow <- rowMeans(T, na.rm=TRUE)
xcol <- colMeans(T, na.rm=TRUE)
matrixmean <- mean(xcol)
matrixmean2 <- mean(xrow)
#
# Double-Center the Matrix Using old Long Method
# Compute comparison as safety check
#
i <- 0
while (i < nrow) {
i <- i + 1
j <- 0
while (j < ncol) {
j <- j + 1
TT[i,j] <- (T[i,j]-xrow[i]-xcol[j]+matrixmean)/(-2) This is the Double-Center Operation
}
}
#
# Run some checks to make sure everything is correct
#
xcheck <- sum(abs(TT-TTT)) This checks to see if both methods are the same numerically
#
#
# Perform Eigenvalue-Eigenvector Decomposition of Double-Centered Matrix
#
ev <- eigen(TT)
#
# Find Point furthest from Center of Space
#
aaa <- sqrt(max((abs(ev$vec[,1]))**2 + (abs(ev$vec[,2]))**2)) These two commands do the same thing
bbb <- sqrt(max(((ev$vec[,1]))**2 + ((ev$vec[,2]))**2))
#
# Weight the Eigenvectors to Scale Space to Unit Circle
#
torgerson1 <- ev$vec[,1]*(1/aaa)*sqrt(ev$val[1])
torgerson2 <- -ev$vec[,2]*(1/aaa)*sqrt(ev$val[2]) Note the Sign Flip
#
plot(torgerson1,torgerson2,type="n",asp=1,
main="",
xlab="",
ylab="",
xlim=c(-3.0,3.0),ylim=c(-3.0,3.0),font=2)
points(torgerson1,torgerson2,pch=16,col="red",font=2)
text(torgerson1,torgerson2,names,pos=namepos,offset=0.2,col="blue",font=2) Experiment with the offset value
#
#
# Main title
mtext("Double-Centered Driving Distance Matrix \n Torgerson Coordinates",side=3,line=1.25,cex=1.5,font=2)
# x-axis title
mtext("West --- East",side=1,line=2.75,cex=1.2,font=2)
# y-axis title
mtext("South --- North",side=2,line=2.5,cex=1.2,font=2)
#
The program will produce a graph that looks similar to this:
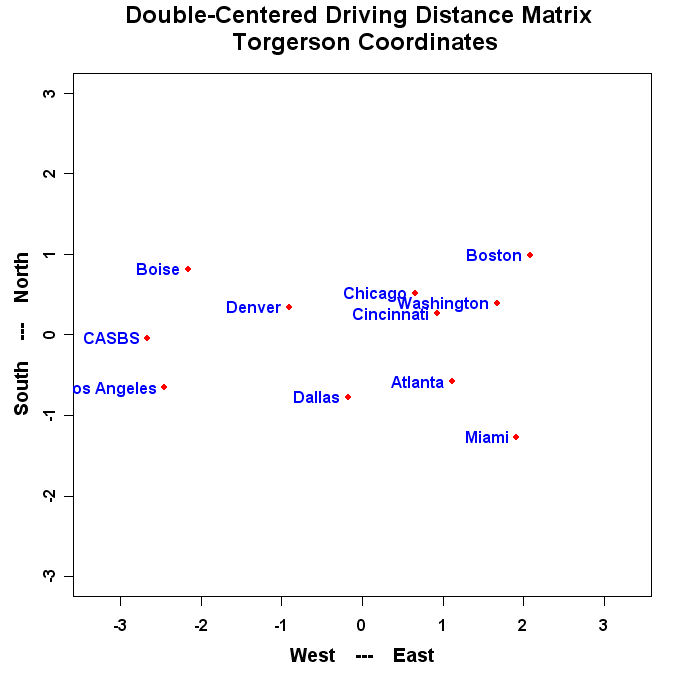
- Run the Program and turn in the resulting plot.
- Change the values in "namepos" until you have a nice looking plot with no overlapping
names and no names cut off by the margins and turn in the resulting plot.
- Add a 12th city (you will have
to get a driving atlas to do this) to Drive2.txt and call the matrix Drive3.txt.
Modify the R program to read and plot the 12 by 12 driving
distance matrix. Turn in Drive3.txt, the resulting plot, and the modified
R program.
The aim of this problem is to show you how to use
R to simulate a complex model of stimulus
evaluation. The idea is that people use a simple mental model to compare
two stimuli. The distinguishing features of the stimuli are assumed to be
represented by dimensions in a simple geometric model. The stimuli are
positioned on the dimensions according to the levels of the
attributes represented by the dimensions. People are assumed to perceive
the stimuli correctly with some
random error. When asked to perform a stimulus comparison, people draw
a momentary psychological value from a very tight error distribution
around the locations of each of the stimuli. Their judgement of similarity
is assumed to be an exponential function of the psychological distance between
the two stimuli -- e-kd -- where d is the distance between
the two momentary psychological values expressed as points in psychological
space, and k is a scaling constant (see the figure below).
What we are going to do is use a program to simulate this process and numerically
compute the
expected value of e-kd for 40 values of
the true distance (from 0 to 2) between the true locations of the stimuli.
Use the following R program below to do this experiment:
Shepard-Ennis-Nofosky_1.r -- Program to
test the Shepard-Ennis_Nofosky Model of Stimulus Comparison
Here is what the program looks like:
#
#
# normal_2.r -- Test of Shepard_Ennis_Nofosky model of Stimulus
# Comparison
#
# Exemplars have bivariate normal distributions. One point is
# drawn from each distribution and the distance computed.
# This distance is then exponentiated -- exp(-d) -- and
# this process is repeated m times to get a E[exp(-d)].
#
# Note that when STDDEVX is set very low then this is equivalent
# to a legislator's ideal point so that the stimulus comparison
# is between the ideal point and the momentary draw from the
# Exemplar distribution.
#
# Set Means and Standard Deviations of Two Bivariate Normal Distributions
#
# Remove all objects just to be safe
#
rm(list=ls(all=TRUE))
#
STDDEVX <- .001 Initialize Means and Standard
STDDEVY <- .4 Deviations of the Two Normal Distributions
XMEAN <- 0
YMEAN <- 0
#
# Set Number of Draws to Get Expected Value
#
m <- 10000
#
# Set Number of Points
#
n <- 40
#
# Set Increment for Distance Between Two Bivariate Normal Distributions
#
XINC <- 0.05 Note that n*XINC = 2.0
#
x <- NULL Initialize vectors
y <- NULL
z <- NULL
xdotval <- NULL
ydotval <- NULL
zdotval <- NULL
iii <- 0
while (iii <= n) { ****Start of Outer Loop -- it Executes Until y has n=40 Entries
x <- 0
i <- 0
iii <- iii + 1
while (i <= m) { ****Start of Inner Loop -- it Executes m=10000 Times
#
# Draw points from the two bivariate normal distributions
# Draw two numbers randomly from Normal Distribution with Mean XMEAN and stnd. dev. of STDDEVX and put them in the vector xdotval
xdotval <- c(rnorm(2,XMEAN,STDDEVX))
ydotval <- c(rnorm(2,YMEAN,STDDEVY))
# Draw two numbers randomly from Normal Distribution with Mean YMEAN and stnd. dev. of STDDEVY and put them in the vector ydotval
# Compute distance Between two randomly drawn points
# Calculate Euclidean Distance Between xdotval and ydotval
zdotval <- sqrt((xdotval[1]-ydotval[1])**2 + (xdotval[2]-ydotval[2])**2)
#
# Exponentiate the distance
#
zdotval <- exp(-zdotval)
#
# Compute Expected Value
#
x <- x + zdotval/m Store exp(-d) in x -- note the division by m so that x will contain
i <- i + 1 the mean after m=10000 trials
} ****End of Inner Loop
#
# Store Expected Value and Distance Between Means of Two Distributions
#
y[iii] <- x
z[iii] <- sqrt(2*YMEAN^2)
YMEAN <- YMEAN + XINC Increment YMEAN by .05
} ****End of Outer Loop
#
# The type="n" tells R to not display anything
#
plot(z,y,xlim=c(0,3),ylim=c(0,.7),type="n",
main="",
xlab="",
ylab="",font=2)
#
# Another Way of Doing the Title
#
#title(main="Test of Shepard-Ennis-Nofosky, .001, .4\nTest of Ideal Point vs. Outcome Model")
# Main title
mtext("Test of Shepard-Ennis-Nofosky, .001, .4\nTest of Ideal Point vs. Outcome Model",side=3,line=1.00,cex=1.2,font=2)
# x-axis title
mtext("True Distance Between Stimuli",side=1,line=2.75,font=2,cex=1.2)
# y-axis title
mtext("Expected Value of Observed Similarity",side=2,line=2.75,font=2,cex=1.2)
##
# An Alternative Way to Plot the Points and the Lines
#
points(z,y,pch=16,col="blue",font=2)
lines(z,y,lty=1,lwd=2,font=2,col="red")
#
The program will produce a graph that looks similar to this:
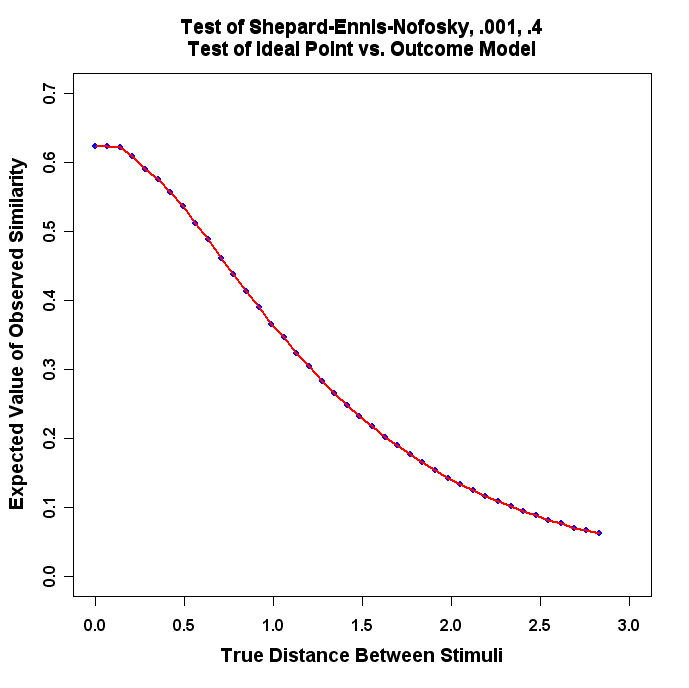
- Run the Program and turn in the resulting plot.
- Change STDDEVX and
STDDEVY
in Shepard-Ennis-Nofosky_1.R, re-load it into R, and produce
a plot like the above. For example, change STDDEVX to .1 and STDDEVY
to .4 and re-run the program. Change the "title" each time to reflect the
different values! Pick 3 pairs of
reasonable values of STDDEVX and STDDEVY and produce plots for
each experiment.
Drive2.txt -- 11 City Driving Distances Data