In problem (1) we used General Purpose Optimization Routine --
optim -- in R to find a
mode that is, hopefully, the global minimum of our
posterior distribution. Now we are
going to use
WINBUGS to analyze
our posterior distribution. (If you need a refresher inWINBUGS go to my Bayes by the
Beach Page and go through the
Gary King Data
Example. It has detailed screen shots of how to use WinBUGS.)
Specifically, we are going to use
RtoWinBUGS
(Download)
(Documentation). Download the R
program and the text files it uses:
 nations_RtoWinbugs.r
-- Program to run the Log-Normal Bayesian Model on the Nations
data.
nations_RtoWinbugs.r
-- Program to run the Log-Normal Bayesian Model on the Nations
data.
Here is the R Program:#
#
# Wish 1971 nations similarities data
# Title: Perceived similarity of nations
#
# Description: Wish (1971) asked 18 students to rate the global
# similarity of different pairs of nations such as 'France and China' on
# a 9-point rating scale ranging from `1=very different' to `9=very
# similar'. The table shows the mean similarity ratings.
#
# Brazil 9.00 4.83 5.28 3.44 4.72 4.50 3.83 3.50 2.39 3.06 5.39 3.17
# Congo 4.83 9.00 4.56 5.00 4.00 4.83 3.33 3.39 4.00 3.39 2.39 3.50
# Cuba 5.28 4.56 9.00 5.17 4.11 4.00 3.61 2.94 5.50 5.44 3.17 5.11
# Egypt 3.44 5.00 5.17 9.00 4.78 5.83 4.67 3.83 4.39 4.39 3.33 4.28
# France 4.72 4.00 4.11 4.78 9.00 3.44 4.00 4.22 3.67 5.06 5.94 4.72
# India 4.50 4.83 4.00 5.83 3.44 9.00 4.11 4.50 4.11 4.50 4.28 4.00
# Israel 3.83 3.33 3.61 4.67 4.00 4.11 9.00 4.83 3.00 4.17 5.94 4.44
# Japan 3.50 3.39 2.94 3.83 4.22 4.50 4.83 9.00 4.17 4.61 6.06 4.28
# China 2.39 4.00 5.50 4.39 3.67 4.11 3.00 4.17 9.00 5.72 2.56 5.06
# USSR 3.06 3.39 5.44 4.39 5.06 4.50 4.17 4.61 5.72 9.00 5.00 6.67
# USA 5.39 2.39 3.17 3.33 5.94 4.28 5.94 6.06 2.56 5.00 9.00 3.56
# Yugoslavia 3.17 3.50 5.11 4.28 4.72 4.00 4.44 4.28 5.06 6.67 3.56 9.00
#
rm(list=ls(all=TRUE))
#
library(arm) The arm library calls a series of other libraries including RtoWinBUGS
setwd("C:/uga_course_homework_6")
#
#
# Read Nations Similarities Data
#
T <- matrix(scan("C:/uga_course_homework_6/nations.txt",0),ncol=12,byrow=TRUE)
TT <- 9-T Note the Subtraction -- We need Distances/Dissimilarities, not Similarities
dim(TT)
#
nrow <- length(TT[,1])
#ncol <- length(TT[1,])
Setup for passing our distances as a List
V <- cbind(TT[,1],TT[,2],TT[,3],TT[,4],TT[,5],TT[,6],TT[,7],TT[,8],TT[,9],TT[,10],TT[,11],TT[,12])
N = nrow
K = ncol(V)
data.data = list(dstar=V) Our distance data as a list
initializing our variables
data.inits = function() {list(x=runif(2*K,-2,2), tau=runif(1,0,10))}
Variables we want analyzed in the WinBUGS Script
data.parameters = c("x","tau","sumllh2")
Here is the call to WinBUGS14
Documentation for the bugs call
wide.sim = bugs(data.data, data.inits, data.parameters,bugs.directory="c:/WinBUGS14/",model.file="nations_bayes_model.txt", n.chains=4, n.thin=1, n.burnin=15000,n.iter=100000, debug=TRUE,digits=5)
#wide.sim = bugs(data.data, inits=NULL, data.parameters,bugs.directory="c:/WinBUGS14/",model.file="nations_bayes_model.txt", n.chains=4, n.thin=1, n.burnin=15000,n.iter=40000, debug=TRUE)
detach(data)
Here is the Model Analyzed by WINBUGS -- nations_bayes_model.txt:
#
# MDS Model for Nations Data
#
model{
#
# Fix USSR Constraints on the USSR and USA
#
x[10,1] <- 0.000
x[10,2] <- 0.000
#
# Fix USA 2nd Dimension
#
x[11,2] <- 0.000
#
for (i in 1:11){ This Loop Computes the Log-Likelihood
llh[i,i] <- 0.0
for (j in i+1:12){
#
#
dstar[i,j] ~ dlnorm(mu[i,j],tau)
mu[i,j] <- log(sqrt((x[i,1]-x[j,1])*(x[i,1]-x[j,1])+(x[i,2]-x[j,2])*(x[i,2]-x[j,2])))
llh[i,j] <- (log(dstar[i,j])-mu[i,j])*(log(dstar[i,j])-mu[i,j])
llh[j,i] <- (log(dstar[i,j])-mu[i,j])*(log(dstar[i,j])-mu[i,j])
}
}
#
# Borrowed From Simon Jackman Simple Trick to Keep track of the log-likelihood
#
llh[12,12] <- 0.0
sumllh2 <- sum(llh[,])
#
## priors Priors on the Parameters
tau ~ dgamma(.1,.1)
#
for(l in 1:2){x[1,l] ~ dnorm(0.0, 0.01)}
x[2,1] ~ dnorm(0.0,0.01)
for(l in 1:2){
for(k in 3:6) {x[k,l] ~ dnorm(0.0, 0.01)}
}
x[7,2] ~ dnorm(0.0,0.01)
x[8,1] ~ dnorm(0.0,0.01)
x[9,2] ~ dnorm(0.0,0.01)
x[11,1] ~ dnorm(0.0,0.01)
for(l in 1:2){x[12,l] ~ dnorm(0.0, 0.01)}
#
# Kludge to fix rotation -- set 1st and 2nd dimension coordinates of
# 4 Nations to fix the sign flips
#
x[2,2] ~ dnorm(0.0,0.01)I(0,) 2nd Dimension Congo > 0
x[7,1] ~ dnorm(0.0,0.01)I(0,) 1st Dimension Israel > 0
x[8,2] ~ dnorm(0.0,0.01)I(,0) 2nd Dimension Japan < 0
x[9,1] ~ dnorm(0.0,0.01)I(,0) 1st Dimension China < 0
}
When you load nations_RtoWinbugs.r into R it starts WinBUGS. You can watch WINBUGS in operation by bringing it to the front
and it should look something like this:
This is what it looks like when it is finished. Note the Path
Statement!!

WinBUGS is still running so you can get
more information about the estimation than is provided in the
default. In particular, we want to see the Density for
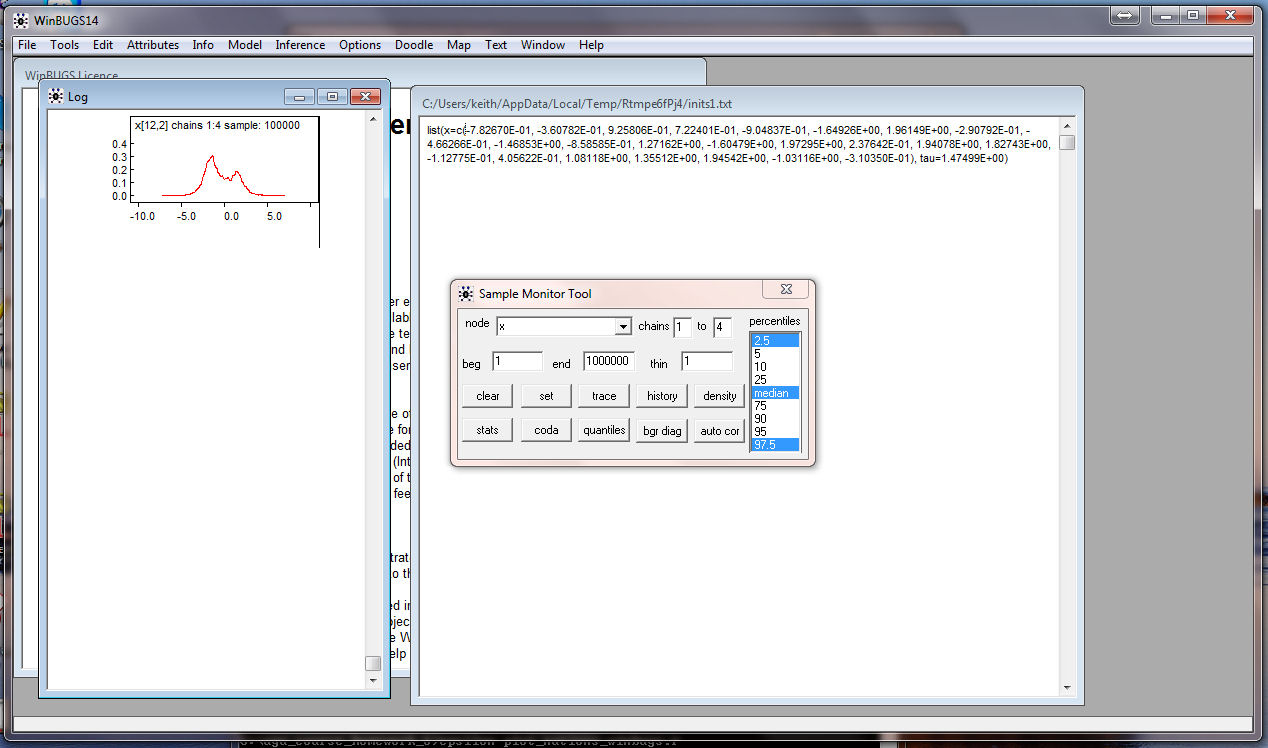
each of the variables. Under Inference select Samples
from the drop-down menu and you get the Sample Monitor Tool

Put x in the node window and click on density and all the
densities for the coordinates appear:
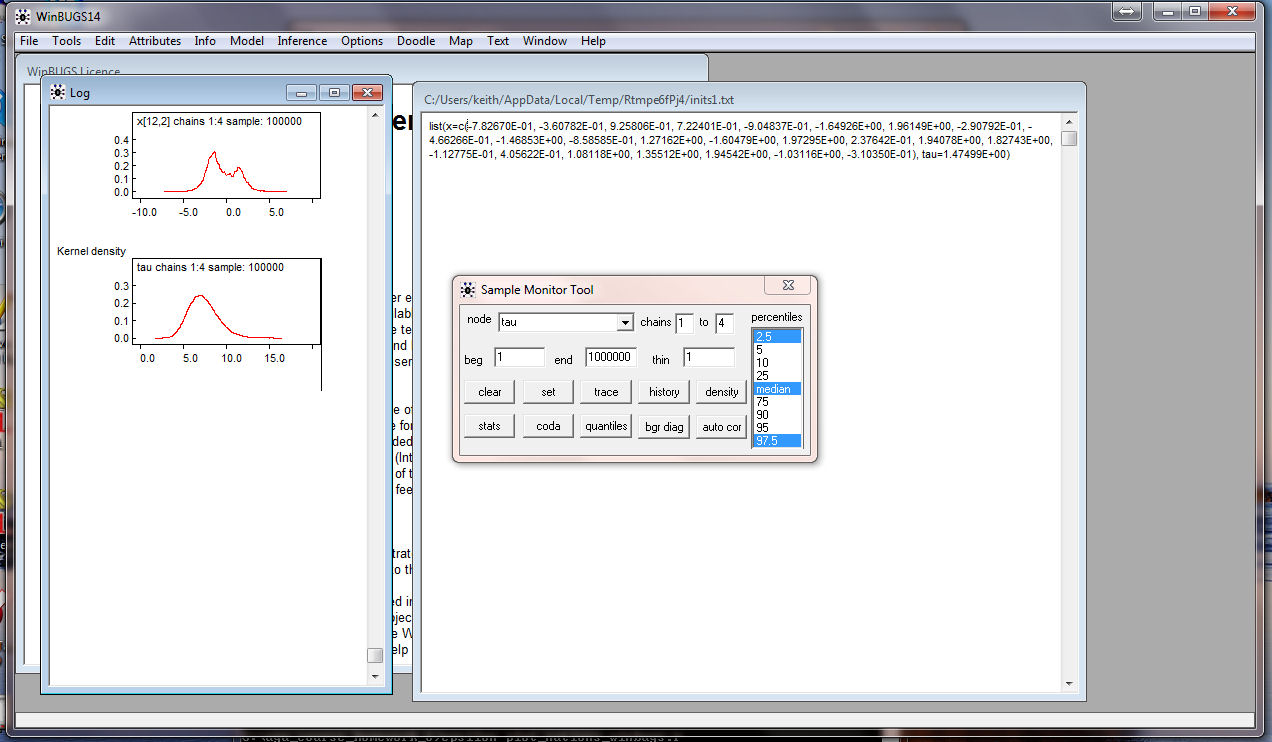
Similarly, get the density for tau:
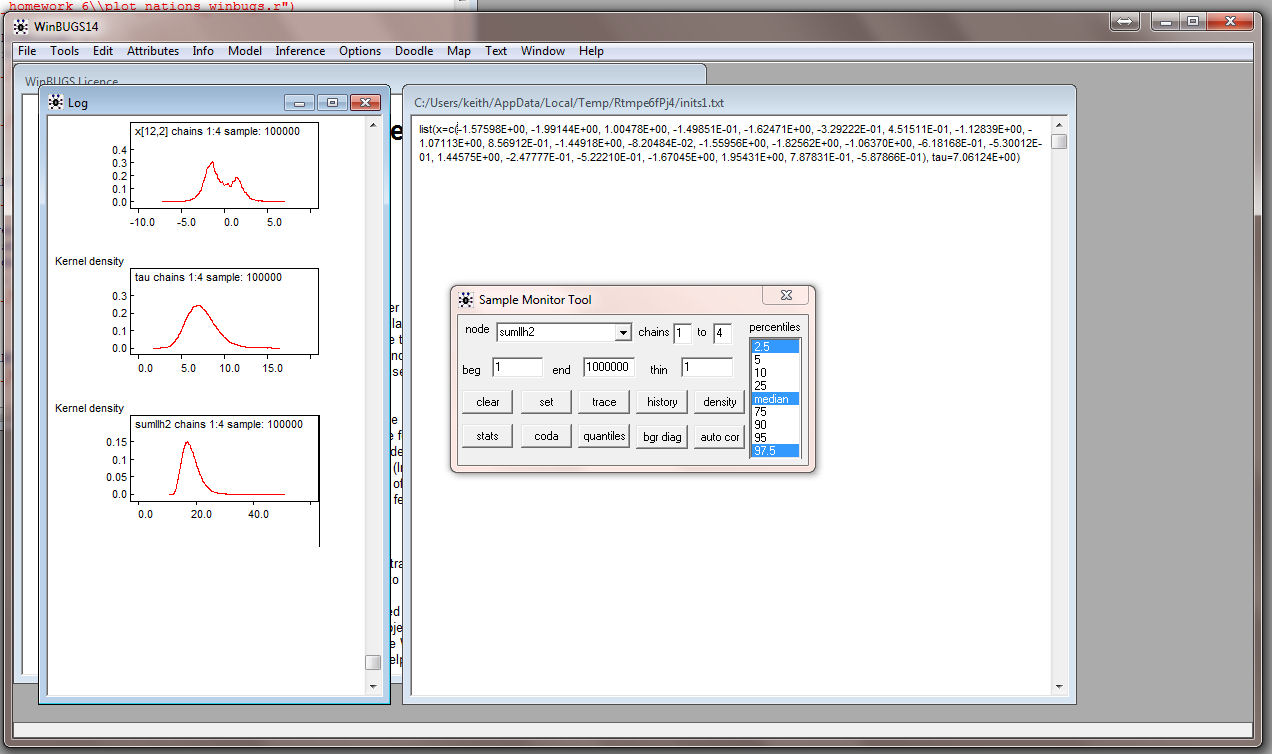
and the density for the log-likelihood (sumllh2):
Be sure to have a Command Prompt running and go to the directory where
WinBUGS has written the output files.
This is what it should look like:
Use Epsilon to bring up
log.txt (we will use this below):

Since we have the densities in the output log file copy log.odc over
to your directory but rename it something like log_10.odc:
Always have a spare copy of WinBUGS
running. You can now open log_10.odc in WinBUGS:

And it should look like this:
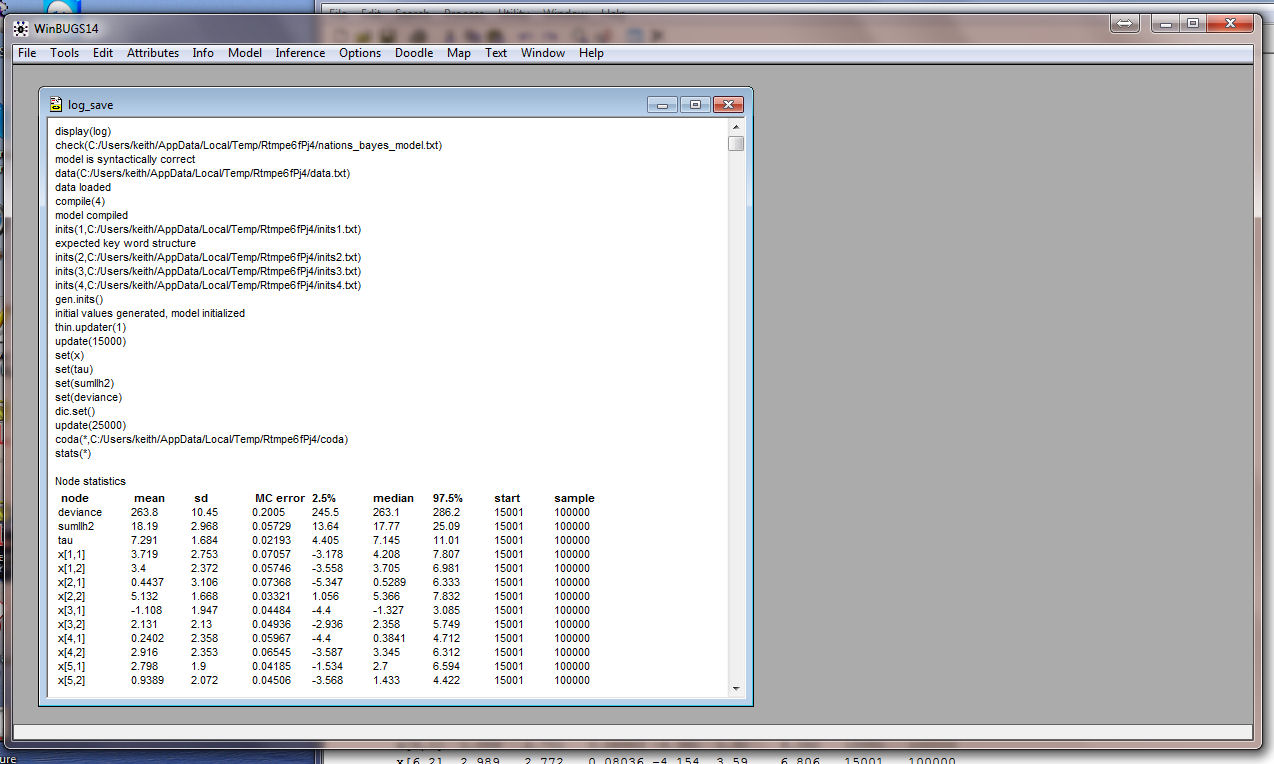
You can copy the Density plots and paste them into MICROSHAFT WORD (be sure to use the Paste Special option):

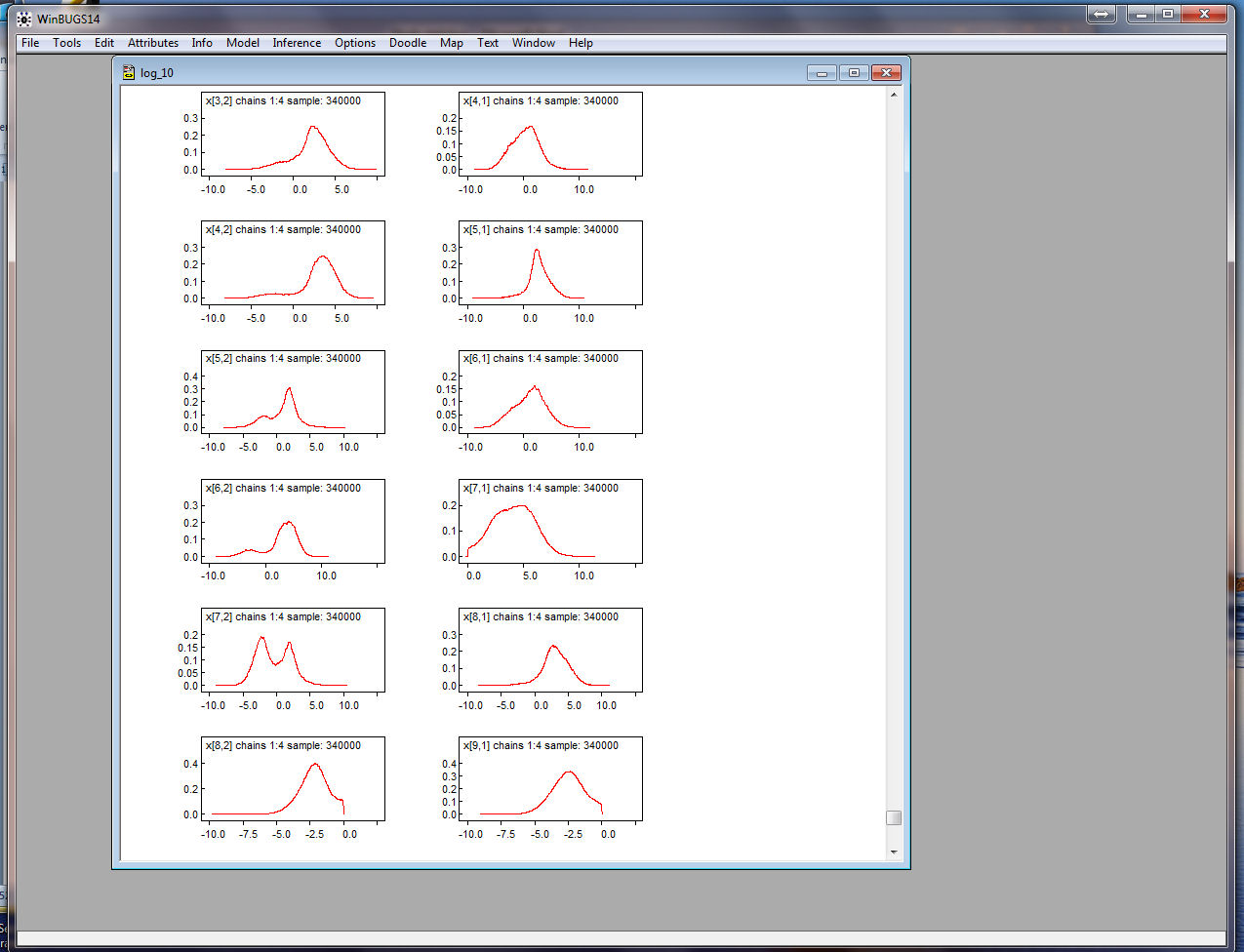
Below are screen shots of the Densities for all of the
parameters:

Note that some of the coordinates have two modes! Also note that you
can pick out those coordinates that have been constrained!

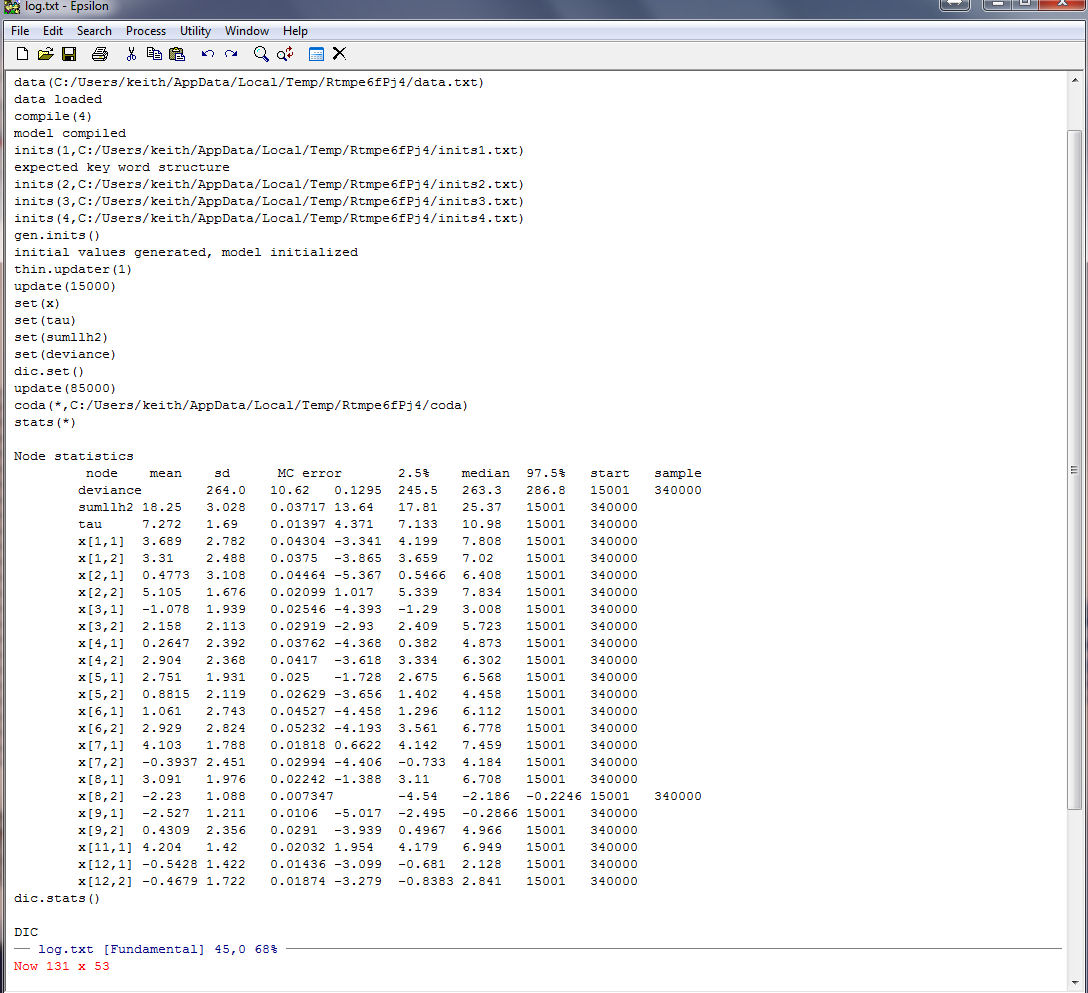
Here are the mean coordinates from our WinBUGS run. Note that the standard errors are
not real great but OK.
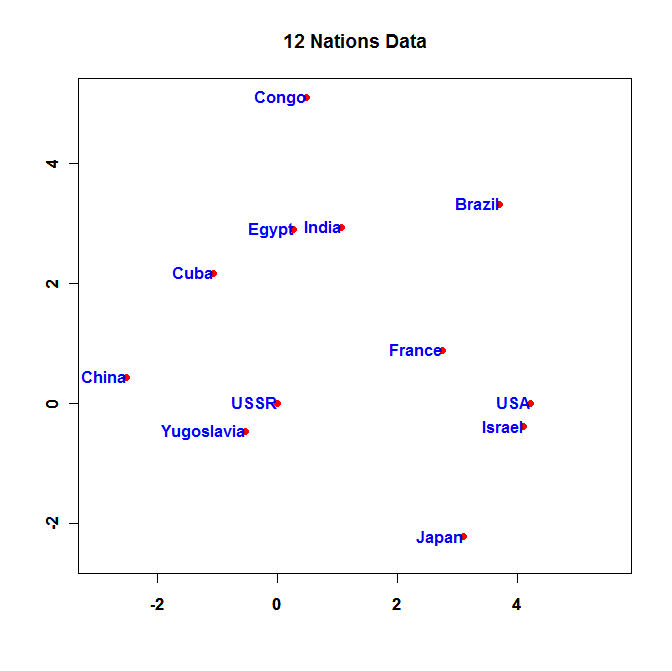
And here is a plot of the Nations from WinBUGS:
- Run the R program above and
put the Node Statistics Table into WORD NEATLY
FORMATTED! Paste in the Densities for Deviance,
sumllh2, and tau. Show every multi-mode coordinate density and
identify the country.
- Neatly graph the mean coordinates from your WinBUGS run and turn in the R code you used to make the plot.
Let A be the matrix of Nation coordinates from question (1) and
B be the matrix of Nation coordinates from question (2). Using the
same method as Question 4 of
Homework 5 solve for the orthogonal procrustes rotation
matrix, T, for B.
- Solve for T and turn in a neatly formatted listing
of T. Compute the Pearson
r-squares between the corresponding columns of A and B before and
after rotating B.
- Do a two panel graph with the two plots side-by-side -- A
on the left and B on the right.
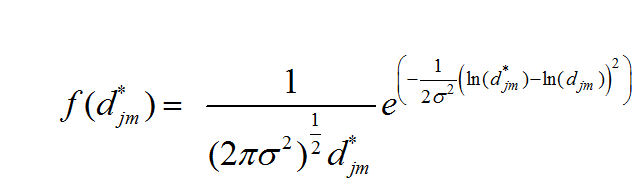
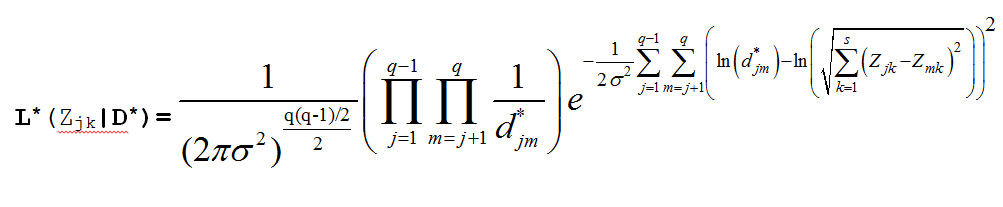
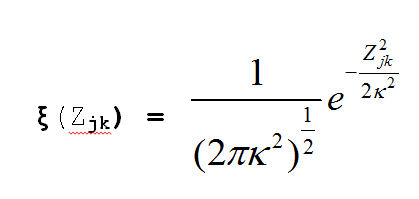
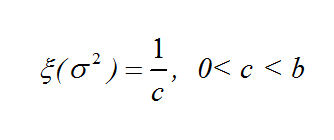
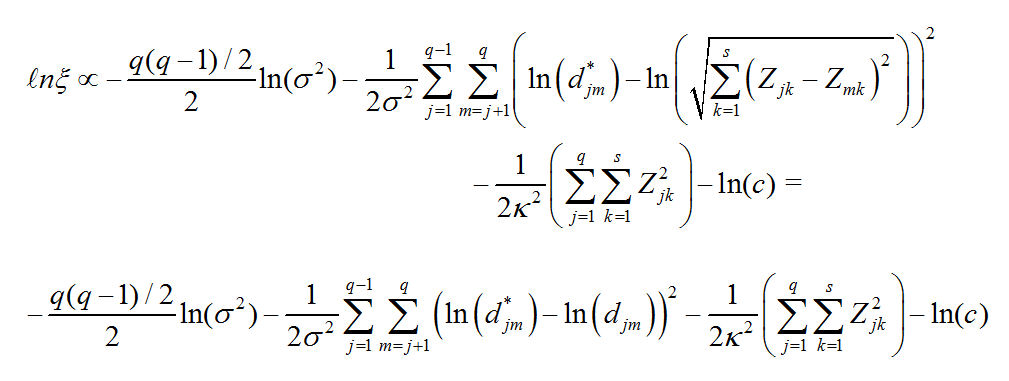
 metric_mds_nations_log_normal_2.r
-- Program to optimize the Log-Normal Bayesian Model for the Nations
data.
metric_mds_nations_log_normal_2.r
-- Program to optimize the Log-Normal Bayesian Model for the Nations
data. nations_RtoWinbugs.r
-- Program to run the Log-Normal Bayesian Model on the Nations
data.
nations_RtoWinbugs.r
-- Program to run the Log-Normal Bayesian Model on the Nations
data. nations_bayes_model.txt
-- Model used by WINBUGS
nations_bayes_model.txt
-- Model used by WINBUGS nations.txt
-- Nations Data used by WINBUGS
nations.txt
-- Nations Data used by WINBUGS















