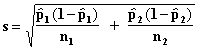LEGACY CONTENT. If you are looking for Voteview.com, PLEASE CLICK HERE

This site is an archived version of Voteview.com archived from University of Georgia on May 23, 2017. This point-in-time capture includes all files publicly linked on Voteview.com at that time. We provide access to this content as a service to ensure that past users of Voteview.com have access to historical files. This content will remain online until at least January 1st, 2018. UCLA provides no warranty or guarantee of access to these files.

45-733 PROBABILITY AND STATISTICS I

A SHORT GUIDE TO CONFIDENCE INTERVALS

 

Confidence        Sample Size           Variance          What Test 
Interval     (Type of Distribution)                         to Use



                                         s2 known            IA Z
             Small Sample (Normal)
                                         s2 unknown          IIIA t
   m

                                         s2 known            IA Z
             Large Sample (Any)
                                         s2 unknown          IIA Z



                                         s2 known            IB Z
             Small Sample (Normal)
                                         s2 unknown          IIIB t
m1 - m2
                                         s2 known            IB Z
             Large Sample (Any)
                                         s2 unknown          IIB Z



   p         Large Sample                NA                  VA Z




p1 - p2       Large Sample                NA                  VB Z




   s2         Small and Large (Normal)    NA                  IV c2
  1. Confidence Intervals for m When s2 is known

    These tests are used when the random sample is drawn from a Normal distribution with a known variance.

    1. Confidence Interval for m

      Confidence Limits

    2. Confidence Interval for the Difference Between Two Means

      In this sampling situation the variances of the two populations are known.

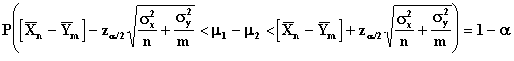
      Confidence Limits


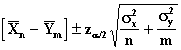
  2. Large Sample Confidence Intervals for m (n ³ 30)

    When the sample size is large, the Central Limit Theorem allows us to calculate confidence intervals for any distribution using these formulas (compare these with the ones for proportions in V).

    1. Confidence Interval for m

      where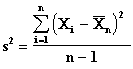

      Confidence Limits

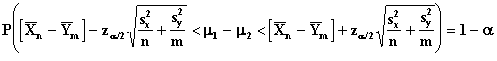
    2. Confidence Interval for the Difference Between Two Means

      Confidence Limits

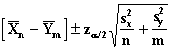
  3. Small Sample Confidence Intervals for m (n £ 29)

    These tests are used when the random sample is drawn from a Normal distribution with unknown variance.

    1. Confidence Interval for m

      where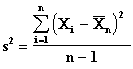

      Confidence Limits

    2. Confidence Interval for the Difference Between Two Means

      In this sampling situation the variances of the two populations are assumed to be the same.

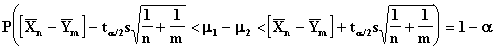
      where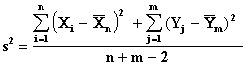

  4. Confidence Interval For s2

    This test is used when the random sample is drawn from a Normal Distribution.

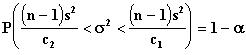
    where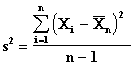

    Confidence Limits 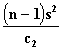and

  5. Large Sample Confidence Intervals For Proportions

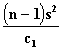
    When the sample size is large, the Central Limit Theorem allows us to calculate confidence intervals for proportions (technically the random sample is drawn from a Bernoulli distribution). Recall that

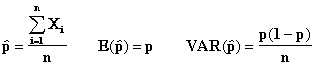
    Using the Central Limit Theorem we assume that

    ~

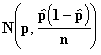
    1. Confidence Interval for p

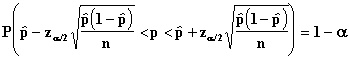
      Confidence Limits

    2. Confidence Interval For the Difference Between Two Proportions

      Let p1 and p2 be the two population proportions and let n and m be the sample sizes from the two populations respectively. Using the Central Limit Theorem we assume that

      ~

       

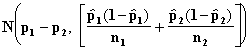
      where