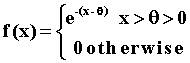
(10 Points)
1. Suppose X has the continuous distribution:
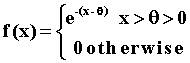
Show that f(x) is a probability distribution.
Clearly, f(x) = e-(x - q) ³ 0(10 Points)
2. You draw a random sample of 11 Pittsburgh crocuses and find that their heights in millimeters are: 5.7, 5.5, 7.5, 6.5, 6.0, 5.5, 7, 6.9, 6.8, 7.1, 7. Assume that the height of Pittsburgh crocuses is normally distributed. Construct 99 percent confidence limits for the true mean height of Pittsburgh crocuses.
n = 11, df = n - 1 = 10, a = .01, a/2 = .005, t.005,10 = 3.169_ Xn = 6.5, s2 = .5The Limits are:
(10 Points)
3. Suppose the bivariate continuous distribution of X and Y is:
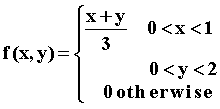
Find VAR(X).
E(X) = (1/3)ò02 ò01x(x + y)dxdy = (1/3)ò02 [x3/3 + (x2y)/2]|01dy =(5 Points)
4. The proportion of people in a large population that have a particular tropical disease is known to be .0004. We take a random sample of 10,000 people. What is the probability that not more than 10 but more than 4 people will have the tropical disease.
Let X be the number of people with the tropical disease. We are given:(10 Points)
5. We are driving through South Dakota during the summer and we see two fields of sunflowers that look very similar. We decide to test our belief that the sunflowers in the two fields are alike so we stop beside the road, walk into the two fields, and measure the heights of a random sample of 11 sunflowers from one field and 13 from the second field. We obtain the following measurements in feet:2.1 3.1 1.9 1.5 2.8 3.3 2.4 2.6 2.7 2.2 3.0 2.9 2.9 and
3.0 1.8 2.8 2.7 2.4 2.3 2.2 3.1 2.9 2.8 2.5
respectively. Assume that the height in both fields is normally distributed. Test the null hypothesis that the variances of the two populations are the same against the alternative hypothesis that the variances are not the same (a = .01).
(10 Points)
6. Two new drugs were given to patients with high blood pressure. The first drug lowered the blood pressure of 13 patients by an average of 38.9 points with a standard deviation of 11.34 points. The second drug lowered the blood pressure of 16 patients by an average of 43.1 points with a standard deviation of 10.55 points. Assume that the two population variances are the same and that the measurements are normally distributed. Test the hypothesis that the two population means are the same against the alternative that they are not the same (a = .01).
df = n + m - 2 = 13 + 16 - 2 = 27, a/2 = .005, t.005,27 = 2.771(10 Points)
7. Suppose X has the continuous probability distribution: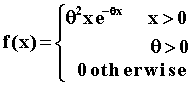
Find the maximum likelihood estimator for q .
fn(x1 , x2 , ... , xn | q) = Pi=1,n q2xi e-qxi = q2n [Pi=1,nxi] e-q åi=1,nxi^ _ Hence, q = 2n/åi=1,nxi = 2/Xn
(10 Points)
8. Suppose we randomly select 10 cards from a standard deck of 52 playing cards. What is the probability that we get 4 cards from one denomination, 3 cards from a second denomination, 2 cards from a third denomination, and 1 card from a fourth denomination.
æ13öæ 4öæ 3öæ 2öæ 1öæ 4öæ 4öæ 4öæ 4ö
ç ÷ç ÷ç ÷ç ÷ç ÷ç ÷ç ÷ç ÷ç ÷
è 4øè 1øè 1øè 1øè 1øè 4øè 3øè 2øè 1ø
-------------------------------
æ52ö
ç ÷
è10ø
(10 Points)
9. Suppose X and Y are independently distributed and that X ~ N(5, 8) and Y ~ N(-10, 25). Find P(3X - 2Y + 18 > 63).(10 Points)
10. A large shipment of carnations is delivered to your flower shop. You take a random sample of 100 carnations and find that 16 are defective. Compute 98 percent confidence limits for the true proportion of defective carnations.
a = .02, a/2 = .01, z.01 = 2.33 ^ ^ ^
Confidence limits: p ± za/2 [p(1 - p)/n]1/2
^
p = 16/100 = .16
Hence, .16 ± 2.33*[(.16*.84)/100]1/2 =
.16 ± .0854(10 Points)
11. Suppose we know that exactly one of the following hypotheses must be true:
H0: m = 110
s 2 = 225
H1: m = 114.9875
The population sampled has a normal distribution and the sample size is 16.
Find a and b
for the decision rule: If ![]() < 114.6875 then do not reject H0:
< 114.6875 then do not reject H0:
If ![]() > 114.6875 then reject H0:
> 114.6875 then reject H0:
_
a = P(Xn > 114.6875 | m = 110) =
_
P[(Xn - m)/(225/16)1/2 > (114.6875-110)/(225/16)1/2] =
P[Z > 1.25] = 1 - F(1.25) = .1056
_
b = P(Xn < 114.6875 | m = 114.9875) =
_
P[(Xn - m)/(225/16)1/2 < (114.6875-114.9875)/(225/16)1/2] =
P[Z < -0.8] = F(-.8) = .4681
(10 Points)
12. Suppose the bivariate discrete distribution of X and Y is: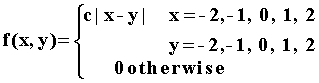
y
-2 -1 0 1 2
---------------------
-2 | 0 1 2 3 4 |10
| |
-1 | 1 0 1 2 3 | 7
| |
x 0 | 2 1 0 1 2 | 6
| |
1 | 3 2 1 0 1 | 7
| |
2 | 4 3 2 1 0 |10
| |
---------------------
10 7 6 7 10 |40
b) Find P(|X - Y| £ 1).
The diagonal of 0's plus the two diagonals of 1's = 8/40.(15 Points)
13. Suppose we flip a coin 500 times. What is the probability that we observe less than 225 heads.(10 Points)
14. A flower arrangement has 20 geraniums. Suppose that the probability that any given geranium will wither is .3 and that the withering of the geraniums are independent of one another. Given that at least 3 geraniums have withered, what is the probability that at most 7 have withered.(10 Points)
15. We take a random sample of 61 Pittsburgh daffodils and measure their heights. We find that the mean height is 7 inches with a standard deviation of .6 inches. Assume that the height of Pittsburgh daffodils is normally distributed. Find 95 percent and 99 percent confidence limits for s2.(10 Points)
16. A survey was conducted by the Sunflower Lovers of America in 1993 and 1997 to determine the popularity of sunflowers in the United States. In 1993 73 percent of 1112 randomly chosen respondents said they loved sunflowers. In 1997 84 percent of 1211 randomly chosen respondents said they loved sunflowers. Do these results indicate a significant difference in the proportions of people who love sunflowers between the two years. Use a = .05. ^ ^
Test statistic: p1 - p2
------------------------- > za/2 or < - za/2
^ ^ ^ ^
[p1(1 - p1)/n1 + p2(1 - p2)/n2]1/2
(.73 - .84)/[(.73*.27)/1112 + (.84*.16)/1211]1/2 =
-6.48