LEGACY CONTENT. If you are looking for Voteview.com, PLEASE CLICK HERE

This site is an archived version of Voteview.com archived from University of Georgia on May 23, 2017. This point-in-time capture includes all files publicly linked on Voteview.com at that time. We provide access to this content as a service to ensure that past users of Voteview.com have access to historical files. This content will remain online until at least January 1st, 2018. UCLA provides no warranty or guarantee of access to these files.

45-734 PROBABILITY AND STATISTICS II Homework Answers #1 (4th Mini AY1997-98)

  1. The model:

    GNP = b 0 + b 1 MILMOB

    where GNP is the % change in GNP and MILMOB is the change in military mobilization is fitted below: (Note: One did not need to transform the given data.)

    ============================================================
LS // Dependent Variable is GNP                                       
Date: 02/28/98   Time: 17:54                                          
Sample: 1915 1988                                                     
Included observations: 74                                             
============================================================
      Variable      CoefficienStd. Errort-Statistic  Prob.            
============================================================
         C           3.025348   0.547696   5.523772   0.0000          
       MILMOB        3.697863   0.547363   6.755782   0.0000          
============================================================
R-squared            0.387966    Mean dependent var 3.061841          
Adjusted R-squared   0.379466    S.D. dependent var 5.980692          
S.E. of regression   4.711230    Akaike info criter 3.126553          
Sum squared resid    1598.089    Schwarz criterion  3.188825          
Log likelihood      -218.6839    F-statistic        45.64060          
Durbin-Watson stat   1.266900    Prob(F-statistic)  0.000000          
============================================================
    1. The estimates for the slope and intercept coefficients are: b1 = 3.698 and b0 = 3.025 respectively. This means that for each unit increase in the variable change in military mobilization the variable change in GNP increases by 3.698 times the change in military mobilization. The 2-tailed observed significance (P-value) of both coefficients is 0, implying that at any reasonable significance level one would reject the null hypotheses Ho: b0 =0 and Ho: b1 =0. In the latter case the null hypothesis for the MILMOB variable specifies that the variable MILMOB has a coefficient 0 in the model and hence has no effect on the variable GNP on the right hand side. The same is true for the constant term. Since we reject both of these hypotheses we can assume that both coefficients are significantly different from 0 which means they are meaningful in the model.

      The residuals of a regression are saved in the variable name by the reserved word RESID after every regression. The EVIEWS command GENR (generate) can be used to save the residuals into a variable called RES, say, as follows:

      GENR RES=RESID

      We can then look at the residuals by typing

      SHOW RES

      in EVIEWS. This display is below.

      The residuals that have absolute values over 9 are in bold: (note there are others with values near 9; 9 is an arbitrary cutoff point.)

                                     RESID
===================================================================
                      Last updated: 02/28/98 - 17:54                         
                                                                             
 1915    3.590703    4.243941   -5.229786   -6.045869    4.284621            
 1920   -1.212403   -5.540562    3.094281    9.495950    0.136206            
 1925   -0.560048    3.289923   -2.058828   -1.831165    2.819159            
 1930   -12.90689   -11.90410   -17.40243   -5.141860    4.353963            
 1935    4.758457    10.08610    1.796987   -7.625791    4.544439            
 1940    4.199656    9.527733    8.606488   -0.239746   -1.300503            
 1945   -6.350234   -0.043979   -1.939323    1.251375   -3.354685            
 1950    5.612538    2.589378    0.021078    1.231581   -3.645527            
 1955    3.335193   -0.593930   -1.236150   -3.282037    2.967425            
 1960   -0.688404   -0.385380    1.580729    1.290056    2.273051            
 1965    2.730666    1.827576   -0.671611    0.785562   -0.391364            
 1970   -2.535118    0.468764    2.575059    2.203462   -3.373036            
 1975   -4.195150    1.858301    1.582365    2.190687   -0.482279            
 1980   -3.190959   -1.124885   -5.614083    0.495162    3.541703            
 1985    0.281572   -0.214503    0.285960    0.777179                        
===================================================================

      The largest residuals are the following:

              1928         9.495950
        1930        12.90689
        1931       -11.90410
        1932       -17.40243
        1942         9.52773
      The model works poorly during the early part of the great depression and in 1942. There were other factors affecting the GNP during the depression besides military mobilization. In 1942, one might surmise that the war was having a positive effect on the economy in the United States, but no real build up of the military had yet occurred as the United States had just entered the war. The residual graph is shown below.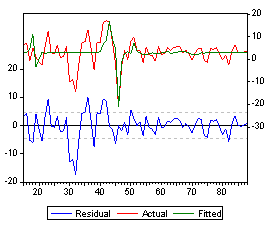

    2. The fact that there was a large military mobilization during World War II and that the GNP also grew quickly at that point in time explains why the actual and predicted values track well at that time. The down "spike" in lines in 1946 is due to the end of world war II. At this point in United States history there was both a large decrease in GNP and a corresponding negative change in military mobilization. This can be checked by using the show command. (The "spike" is due to the large decrease in GNP which is the dependent variable in this problem.)

      ========================================================
OBS       YEAR       MILMOB       GNP         RESID     
========================================================
 2      1946.000   -6.516724   -21.11658   -0.043979
    3. The following regressions were run after using the SMPL command:

      ============================================================
LS // Dependent Variable is GNP                                       
Date: 02/28/98   Time: 18:10                                          
Sample: 1915 1945                                                     
Included observations: 31                                             
============================================================
      Variable      CoefficienStd. Errort-Statistic  Prob.            
============================================================
         C           2.834469   1.281825   2.211276   0.0351          
       MILMOB        3.594665   1.330917   2.700893   0.0114          
============================================================
R-squared            0.200988    Mean dependent var 3.819669          
Adjusted R-squared   0.173436    S.D. dependent var 7.525475          
S.E. of regression   6.841829    Akaike info criter 3.908451          
Sum squared resid    1357.508    Schwarz criterion  4.000966          
Log likelihood      -102.5681    F-statistic        7.294821          
Durbin-Watson stat   1.101443    Prob(F-statistic)  0.011426          
============================================================



============================================================
LS // Dependent Variable is GNP                                       
Date: 02/28/98   Time: 18:11                                          
Sample: 1947 1988                                                     
Included observations: 42                                             
============================================================
      Variable      CoefficienStd. Errort-Statistic  Prob.            
============================================================
         C           3.235515   0.372849   8.677815   0.0000          
       MILMOB        5.290072   1.427013   3.707093   0.0006          
============================================================
R-squared            0.255711    Mean dependent var 3.078169          
Adjusted R-squared   0.237103    S.D. dependent var 2.748479          
S.E. of regression   2.400630    Akaike info criter 1.797910          
Sum squared resid    230.5210    Schwarz criterion  1.880657          
Log likelihood      -95.35153    F-statistic        13.74254          
Durbin-Watson stat   2.112150    Prob(F-statistic)  0.000635          
============================================================
      In both regressions the slope coefficient of MILMOB is significant, i.e. significantly different from 0. However, after World War II the effect of MILMOB on the change in GNP is even greater. It is 5.29*change in MILMOB after 1945 as compare to 3.59*change in MILMOB before 1945. The value of this coefficient in the original (whole data set) regression was very close to that in the pre 1945 regression, but somewhat different from the post 1945 regression results. The R coefficients are not high in either case, which indicates that the data do not fit the linear model all that well. However, assuming these models do work one might say the effect of military mobilization on the economy is even greater since World War II.
  2. Problem 11.2 MWS Working Directly With a Calculator

    åi=1,10 Xi = 720,    åi=1,10 Xi2 = 106554,   
    åi=1,10 Yi = 721,    åi=1,10 Yi2 = 105817,    åi=1,10 XiYi = 106155    

            ^    106155 - (1/10)*720*721    54243
Hence   b1 = ----------------------- = ------- = .9913916
             106554 - (1/10)*720*720    54714
        ^
  and   b0 = 721/10 - .9913916*(720/10) = .7198048

The least squares straight line is:
        ^   ^    ^
  and   y = b0 + b1x = .7198048 + .9913916*x

The expected change in audited value (y) for a one-unit change in 
                     ^  
  book value (x), is b1 = .9913916

When x = 100, the best estimate of y is
        ^ 
  and   y = .7198048 + .9913916*100 = 99.858965
  3. Problem 11.2 MWS EVIEWS

    Below is the EVIEWS output for problem 11.2: 
    
============================================================
LS // Dependent Variable is Y                                         
Date: 02/28/98   Time: 18:21                                          
Sample: 1 10                                                          
Included observations: 10                                             
============================================================
      Variable      CoefficienStd. Errort-Statistic  Prob.            
============================================================
         C           0.719805   1.176355   0.611894   0.5576          
         X           0.991392   0.011396   86.99447   0.0000          
============================================================
R-squared            0.998944    Mean dependent var 72.10000          
Adjusted R-squared   0.998812    S.D. dependent var 77.33973          
S.E. of regression   2.665648    Akaike info criter 2.137751          
Sum squared resid    56.84544    Schwarz criterion  2.198268          
Log likelihood      -22.87814    F-statistic        7568.037          
Durbin-Watson stat   2.455810    Prob(F-statistic)  0.000000          
============================================================