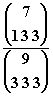
45-733 Probability and Statistics I (3rd Mini AY 1999-2000 Flex-Mode and Flex-Time)
Assignment#2 Answers
æ3öæ5ö
ç ÷ç ÷
è2øè2ø
P(E) = ---------
æ8ö
ç ÷
è4ø
2.37 Clearly, there are [52 choose 2]
outcomes. There are 4 Aces and there are 12 Face cards
(i.e., Jacks, Queens, Kings). Hence,
æ4öæ12ö
ç ÷ç ÷
è1øè 1ø
P(E) = ---------
æ52ö
ç ÷
è 2ø
2.38 The number of ways to divide the 9 motors between the three production lines is
P(two to first line) =
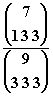
![]() =
=
![]()
P(M | Pc) =
![]()
=
![]() = .4
= .4
P(A | F) =
![]()
=
*
![]() = 14/17
= 14/17