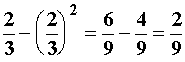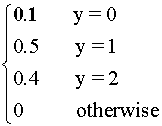
45-733 Probability and Statistics I (3rd Mini AY 1999-2000 Flex-Mode and Flex-Time)
Assignment#3 Answers
3.2 The sample space is:
S = {HH, HT, TH, TT}
and the corresponding values of Y are 2, -1, -1, and
1, respectively.
Now, since each outcome in S is equally likely
{ 1/2 y = -1
{
{ 1/4 y = 1
f(y) = {
{ 1/4 y = 2
{
{ 0 otherwise
{ 1/6 y = 2
{
{ 2/6 y = 3
f(y) = {
{ 3/6 y = 4
{
{ 0 otherwise
A B C Y
---------------------
A B C 3
A C B 1
B A C 1
B C A 0
C A B 0
C B A 1
Hence, P(0) = 2/6 = 1/3, P(1) = 3/6 = 1/2,
{ 1/3 y = 0
{
{ 1/2 y = 1
{
f(y) = { 0 y = 2
{
{ 1/6 y = 3
{
{ 0 otherwise
{ 4/9 x1 = 0 { 4/9 x2 = 0
{ {
{ 4/9 x1 = 1 { 4/9 x2 = 1
f(x1) = { f(x2) = {
{ 1/9 x1 = 2 { 1/9 x2 = 2
{ {
{ 0 otherwise { 0 otherwise
{ .001 y = 85,000
{
{ .01 y = 42,500
f(y) = {
{ .989 y = 0
{
{ 0 otherwise
f(y) = 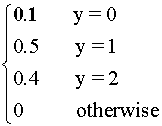
Let X = Daily Cost = 10Y, then
4.3 Given
f(y) = 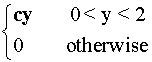
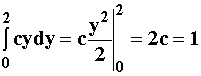
![]()
F(y) = P(Y<y) =
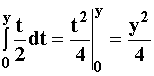
F(y) = 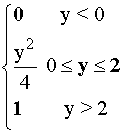
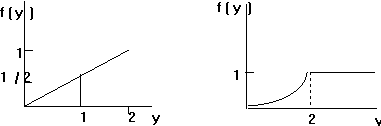
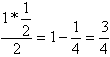
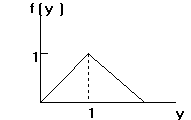
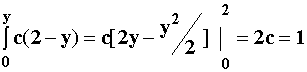 Þ
c =
Þ
c = ![]()
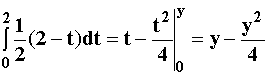 Hence:
Hence:F(y) = 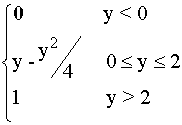
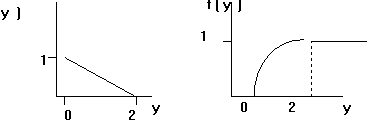
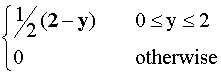
E[Y] =
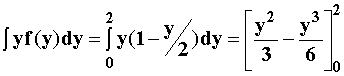 =
= E[Y2] =
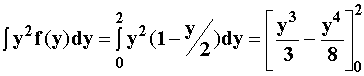 =
= VAR[Y] =