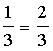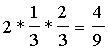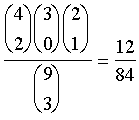 and so on.
and so on.45-733 Probability and Statistics I (3rd Mini AY 1999-2000 Flex-Mode and Flex-Time)
Assignment #4 Answers
Y2
1 2 3
------------
1 | 1 2 1 | 4
| |
Y1 2 | 2 2 0 | 4
| |
3 | 1 0 0 | 1
| |
---------------
4 4 1 | 9
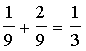
Y2 = Side Bet
-1 1 2 3
--------------
0 | 1 0 0 0 | 1
| |
1 | 0 1 1 1 | 3
Y1 | |
2 | 0 2 1 0 | 3
| |
3 | 0 1 0 0 | 1
| |
----------------
1 4 2 1 | 8
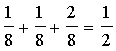
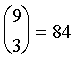 elements. Ranges:
elements. Ranges:P(Y1=2, Y2=0) = f(y1=2, y2=0) =
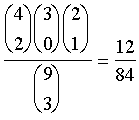 and so on.
and so on.
Y2
0 1 2 3
--------------
0 | 0 3 6 1 | 10
| |
1 | 4 24 12 0 | 40
Y1 | |
2 |12 18 0 0 | 30
| |
3 | 4 0 0 0 | 4
| |
----------------
20 45 18 1 | 84
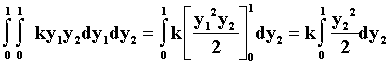 =
[k(y22)/4]|01 = k/4
=
[k(y22)/4]|01 = k/4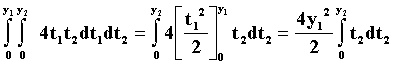
= 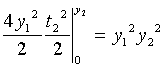
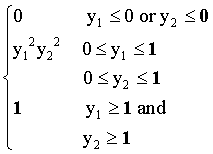
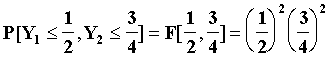 =
= 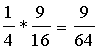
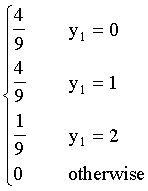
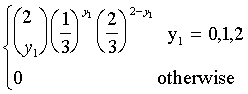
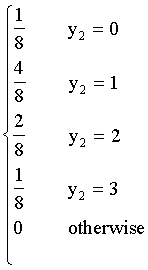
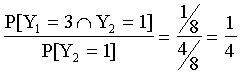
{ 10/84 y1 = 0
{
{ 40/84 y1 = 1
{
f(y1) = { 30/84 y1 = 2
{
{ 4/84 y1 = 3
{
{ 0 otherwise
æ4öæ2öæ3ö
ç ÷ç ÷ç ÷
è1øè1øè1ø
P(Y3 = 1 Ç Y2 = 1) = --------
æ9ö
ç ÷
è3ø
(d) The probabilities are identical.