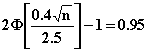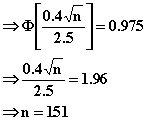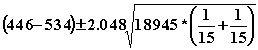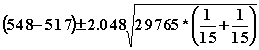LEGACY CONTENT.
If you are looking for Voteview.com, PLEASE CLICK HEREThis site is an archived version of Voteview.com archived from University of Georgia on
May 23, 2017. This point-in-time capture includes all files publicly linked on Voteview.com at that time. We provide access to this content as a service to ensure that past users of Voteview.com have access to historical files. This content will remain online until at least
January 1st, 2018. UCLA provides no warranty or guarantee of access to these files.
45-733 Probability and Statistics I
(3rd Mini AY 1997-98 Flex-Mode and Flex-Time)
Assignment #6 Answers
7.19 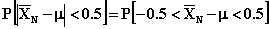 =
=
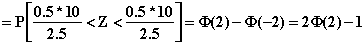 =
2*0.9773 - 1 = 0.9546
=
2*0.9773 - 1 = 0.9546
7.20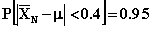
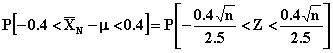 =
=
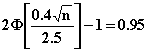
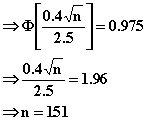
7.21 We are given: m = 5.00,
s = .50, and n = 64. We are
asked to compute:
_
P(Xn £ 4.90) = P[Z £ (4.90 - 5.00)/.5/8] =
P(Z £ -1.6) = F(-1.6) = .0548
8.40(a) 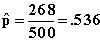
1-a = 0.98,
a = 0.02,
a/2 = 0.01,
Z0.01 = 2.33
Confidence limits are :

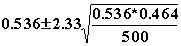
98 % confidence limits are (0.484,0.588)
(b) Yes. There is no evidence that the graduation rate has changed.
8.41 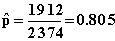
1-a = 0.99,
a = 0.01,
a/2 = 0.005,
Z0.005 = 2.58
Confidence limits are :

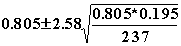
98 % confidence limits are (0.784,0.826)
^
8.43(a) We are given p = 2/3, n = 224, a = .10, Z.05 = 1.645
^ ^ ^
p ± Za/2[p(1 - p)/n] = 2/3 ± 1.645{[(2/3)(1/3)]/224}1/2 =
.667 ± .052 = (.615, .719)
(b) Because the entire interval is greater than 1/2, it is reasonable
to believe that most of the children think that they would like to travel
in space.
8.45 1-a = 0.95,
a = 0.05,
a/2 = 0.025,
Z0.025 = 1.96,
m = 30, n = 30
Use large sample confidence interval

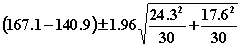
or (15.72, 36.677)
8.51 Large sample CLT proportions
1-a = 0.98,
a = 0.02,
a/2 = 0.01,
Z0.01 = 2.33
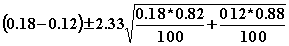
or (-0.05, 0.18)
8.74(a) 1-a = 0.95,
a = 0.05,
a/2 = 0.025,
t0.025 = 2.048 (28 degrees of freedom)
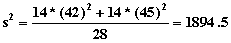
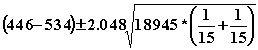
or (-120.55, -55.45)
(b) 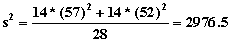
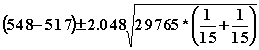
or (-9.8, 71.8)
(c) For the verbal scores, the confidence limits are below 0
indicating that the two populations differ.
For the math scores, 0 is in the interval, so there is not evidence to
conclude that there is a difference.
(d) Must assume samples are drawn from a NORMAL distribution.
8.86 From the data stated in the problem we can calculate:
s2 = 144.5, a = .01,
a/2 = .005,
C1 = .20699, C2 = 14.8602.
The 99% confidence interval for s2 is:
P[(n - 1)s2]/C2 < s2 <
[(n - 1)s2]/C1] = .99
And the endpoints of the interval are: (4*144.5)/14.8602 = 38.9 and
(4*144.5)/.20699 = 2792.41
which produces the interval for the standard deviation of:
6.24 < s < 52.84
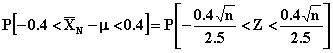 =
=