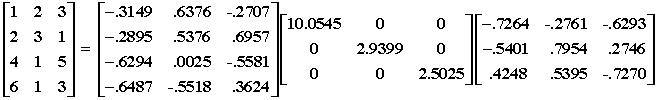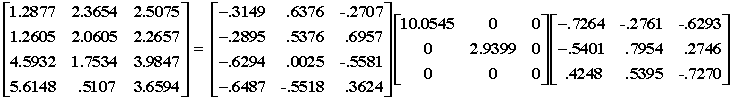LEGACY CONTENT.
If you are looking for Voteview.com, PLEASE CLICK HEREThis site is an archived version of Voteview.com archived from University of Georgia on
May 23, 2017. This point-in-time capture includes all files publicly linked on Voteview.com at that time. We provide access to this content as a service to ensure that past users of Voteview.com have access to historical files. This content will remain online until at least
January 1st, 2018. UCLA provides no warranty or guarantee of access to these files.



The Eckart-Young Theorem
The Eckart-Young Theorem: Given an n by m matrix X of rank
r £ m £ n,
and its singular value decomposition,
ULV', where
U is an n by m matrix,
L is an m by m diagonal matrix of singular values,
and V is an m by m matrix such that
U'U = In and
V'V = VV' = Im
with the
singular values arranged in decreasing sequence
l1 ³
l2 ³
l3 ³ ...
³
lm ³ 0
then there exists an n by m matrix B of rank s,
s £ r, which minimizes the sum of the squared
error between the elements of X and the corresponding elements of
B when
B = ULsV'
where the diagonal elements of the m by m diagonal matrix
Ls are
l1 ³
l2 ³
l3 ³ ...
³
ls >
ls+1 =
ls+2 = ... =
lm = 0
Geometrically, the Eckart-Young Theorem states that the least squares
approximation in s dimensions of a matrix X can be found by replacing
the smallest m-s roots of
L with zeroes and remultiplying
ULV'.
For example, given:
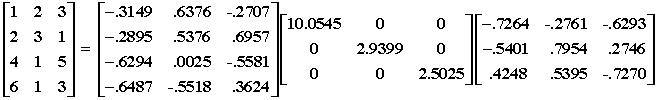
the rank 2 approximation is:
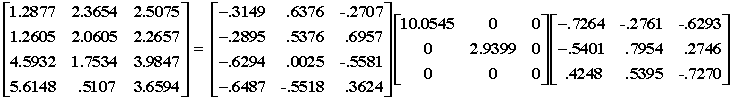
 svd_example.r -- R
Program to illustrate simple SVD.
svd_example.r -- R
Program to illustrate simple SVD.
svd_example.r looks like this:#
# file: svd_example.r
#
# Purpose: Simple R program showing Singular
# Value Decomposition
#
#
rm(list=ls(all=TRUE))
#
#
rc.file <- "c:/ucsd_course/svd_matrix.txt"
#
# Standard fields and their widths
#
rc.fields <- c("y1","y2","y3")
#
rc.fieldWidths <- c(3,3,3)
#
# Read the vote data from fwf
#
T <- read.fwf(file=rc.file,widths=rc.fieldWidths,as.is=TRUE,col.names=rc.fields)
dim(T)
#
nrow <- length(T[,1])
ncol <- length(T[1,])
#
xsvd <- svd(T)
#
# The Two Lines Below Put the Singular Values in a
# Diagonal Matrix -- The first one creates an
# identity matrix and the second command puts
# the singular values on the diagonal
#
Lambda <- diag(ncol)
diag(Lambda) <- xsvd$d
#
# Compute U*LAMBDA*V' for check below
#
XX <- xsvd$u %*% Lambda %*% t(xsvd$v)
#
xerror <- sum(abs(T-XX))
#