1998 Prob-Stat I Midterm Answers Page

LEGACY CONTENT. If you are looking for Voteview.com, PLEASE CLICK HERE

This site is an archived version of Voteview.com archived from University of Georgia on May 23, 2017. This point-in-time capture includes all files publicly linked on Voteview.com at that time. We provide access to this content as a service to ensure that past users of Voteview.com have access to historical files. This content will remain online until at least January 1st, 2018. UCLA provides no warranty or guarantee of access to these files.

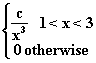
45-733 PROBABILITY AND STATISTICS I 1998 Midterm Examination Answers

Probability and Statistics Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Midterm
Keith Poole

(10 Points)

1. Suppose we have the continuous probability distribution

f(x) =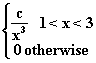

Find c.

ò₁³ (c/x³)dx = (c/-2)(x^-2|₁³ = (c/-2)(1/9 - 1) = (4/9)c; hence, c = 9/4

Find F(x).

F(x) = ò₁^x (9/4t³)dt = (-9/8t²)|₁^x = (9/8)(1 - 1/x²)
Hence

                           {  0                  x <= 1                   
                           {                                 
                    F(x) = {  (9/8)[1 - 1/x**2]  1 < x < 3                 
                           {                               
                           {  1                  x >= 3

Find P(X > 2)

P(X > 2) = 1 - F(2) = 1 - 27/32 = 5/32

Probability and Statistics Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Midterm
Keith Poole

(10 Points)

2. You draw 3 cards randomly without replacement from a deck of 52 playing cards. What is the probability that the 3 cards are from different suits?

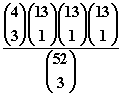
Probability and Statistics Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Midterm
Keith Poole

(10 Points)

3. Suppose we have the bivariate discrete probability distribution:

f(x,y) =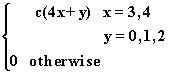

Find c

                               y

                           0   1   2
                         ------------
                       3 |12  13  14 |39
                         |           |
                    x    |           |  
                         |           |
                       4 |16  17  18 |51
                         |           |
                         ---------------
                          28  30  32 |90

Hence, c = 1/90

Are X, Y independent?

No. f(3, 0) = 12/90 ¹ f₁(3)f₂(0) = (39/90)(28/90).

Probability and Statistics Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Midterm
Keith Poole

(10 Points)

4. Suppose we have two urns. In the first urn there are 10 Red and 10 Black balls. In the second urn there are 5 Red and 15 Black balls. One ball is drawn randomly without replacement from each urn. Let Y equal the number of black balls drawn from the two urns.

What is the probability distribution of Y.

P(Y = 0) = (10/20)(5/20) = 50/400
P(Y = 1) = (10/20)(5/20) + (10/20)(15/20) = 200/400
P(Y = 2) = (10/20)(15/20) = 150/400

                           {  50/400   y = 0                   
                           {                                 
                    f(y) = { 200/400   y = 1
                           {                               
                           { 150/400   y = 2

What is E(Y).

E(Y) = 0(50/400) + 1(200/400) + 2(150/400) = 5/4

Probability and Statistics Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Midterm
Keith Poole

(10 Points)

5. Suppose we have a discrete bivariate probability distribution

f(x,y) =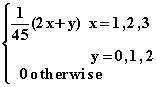

                               y

                           0   1   2
                         ------------
                       1 | 2   3   4 | 9
                         |           |
                    x  2 | 4   5   6 |15
                         |           |
                       3 | 6   7   8 |21
                         |           |
                         ---------------
                          12  15  18 |45

Find P(X > 1 Ç Y > 1)

P(X > 1 Ç Y > 1) = 6/45 + 8/45 = 14/45

Find P(X £ 2 ½ Y £ 1)

P(X £ 2 ½ Y £ 1) = P(X £ 2 Ç Y £ 1)/P(Y £ 1)

P(X £ 2 Ç Y £ 1) = 2/45 + 3/45 + 4/45 + 5/45 = 14/45

P(Y £ 1) = 12/45 + 15/45 = 27/45

Hence, P(X £ 2 ½ Y £ 1) = (14/45)/(27/45) = 14/27

Probability and Statistics Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Midterm
Keith Poole

(10 Points)

6. Suppose there is a new test for detecting a specific disease. One person in every 5000 is known to have the disease. If a person has the disease the probability of a positive test is .99. If a person does not have the disease the probability of a positive test is .15. A person is randomly drawn from a large population and the test is applied to the person. If the test is positive what is the probability that the person does not have the disease?

Probability and Statistics Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Midterm
Keith Poole

(10 Points)

7. An urn contains 6 red and 4 white balls. Three balls are randomly drawn without replacement from the urn. Find the probability that all 3 of the removed balls are red if it is known that at least 1 of the removed balls is red.

Let X = The number of Red balls. Then
P(X = 3 | X ³ 1) = P(X = 3 Ç X ³ 1) = P(X = 3)/P(X ³ 1) = P(X = 3)/[1 - P(X = 0)]

P(X = 3) = [6 choose 3]/[10 choose 3]
P(X = 0) = [4 choose 3]/[10 choose 3]

Hence P(X = 3 | X ³ 1) = [6 choose 3]/{[10 choose 3] - [4 choose 3]}

Probability and Statistics Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Midterm
Keith Poole

(10 Points)

8. Suppose we have the bivariate continuous probability function

f(x,y) =

Find COV(X, Y)

E(X) = ò₀¹ ò₀¹ x(4/7)(2 - xy)dydx = (4/7)ò₀¹ [(2xy - x²y²/2)|₀¹]dx =
(4/7)ò₀¹ (2x - x²/2)dx = (4/7)[x² - x³/6)|₀¹] = (4/7)(1 - 1/6) = 10/21

E(Y) = ò₀¹ ò₀¹ y(4/7)(2 - xy)dxdy = (4/7)ò₀¹ [(2xy - x²y²/2)|₀¹]dy =
(4/7)ò₀¹ (2y - y²/2)dy = (4/7)[y² - y³/6)|₀¹] = (4/7)(1 - 1/6) = 10/21

E(XY) = ò₀¹ ò₀¹ xy(4/7)(2 - xy)dydx = (4/7)ò₀¹ [(xy² - x²y³/3)|₀¹]dx =
(4/7)ò₀¹ (x - x²/3)dx = (4/7)[x²/2 - x³/9)|₀¹] = (4/7)(1/2 - 1/9) = 2/9

COV(X, Y) = E(XY) - E(X)E(Y) = 2/9 - (10/21)(10/21)

Probability and Statistics Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Midterm
Keith Poole

(10 Points)

9. Suppose we have the continuous bivariate probability distribution

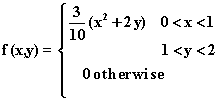
Find VAR(X) and VAR(Y).

E(X) = ò₀¹ ò₁² x(3/10)(x² + 2y)dydx = (3/10)ò₀¹ [(x³y + xy²)|₁²]dx =
(3/10)ò₀¹ (x³ + 3x)dx = (3/10)[x⁴/4 + 3x²/2)|₀¹] = (3/10)(1/4 + 3/2) = 21/40

E(X²) = ò₀¹ ò₁² x²(3/10)(x² + 2y)dydx = (3/10)ò₀¹ [(x⁴y + x²y²)|₁²]dx =
(3/10)ò₀¹ (x⁴ + 3x²)dx = (3/10)[x⁵/5 + x³)|₀¹] = (3/10)(1/5 + 1) = 18/50

E(Y) = ò₁² ò₀¹ y(3/10)(x² + 2y)dxdy = (3/10)ò₁² [(yx³/3 + 2y²x)|₀¹]dy =
(3/10)ò₁² (y/3 + 2y²)dy = (3/10)[y²/6 + 2y³/3)|₁²] = (3/10)(3/6 + 14/3) = 93/60

E(Y²) = ò₁² ò₀¹ y²(3/10)(x² + 2y)dxdy = (3/10)ò₁² [(y²x³/3 + 2y³x)|₀¹]dy =
(3/10)ò₁² (y²/3 + 2y³)dy = (3/10)[y³/9 + y⁴/2)|₁²] = (3/10)(7/9 + 15/2) = 149/60

VAR(X) = 18/50 -(21/40)² = .0844

VAR(Y) = 149/60 -(93/60)² = .0808

Probability and Statistics Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Midterm
Keith Poole

(10 Points)

10. The manager of a stockroom in a factory has constructed the following probability distribution for the daily demand (number of times used) for a particular tool.

                           {  .1   x = 0                   
                           {                                 
                           {  .2   x = 1
                           {                               
                    f(x) = {  .3   x = 2
                           {                               
                           {  .4   x = 3
                           {
                           {  0 otherwise

It costs the factory $10 each time the tool is used. Find the mean and the variance of the daily cost of the tool.

Let Y = 10X

E(X) = 0*.1 + 1*.2 + 2*.3 + 3*.4 = 2

E(X²) = 0*.1 + 1*.2 + 4*.3 + 9*.4 = 5.0

E(Y) = E(10X) = 10E(X) = 10*2 = 20

VAR(Y) = VAR(10X) = 100VAR(X) = 100(5 - 2²) = 100