Here is what Weisberg_and_Rusk_Shepard_Plot.r looks like:
#
#
#
# Weisberg_and_Rusk.r -- Replicates Famous 1970 W&R paper in APSR
#
# ***See Homework #5 2003 Houston MEASUREMENT THEORY Course***
# http://voteview.org/measure.htm
#
# wallace wallace therm
# humphrey humphrey thermometer
# nixon nixon thermometer
# mccarthy mccarthy thermometer
# reagan reagan thermometer
# rockefeller rockefeller thermometer
# lbj lbj thermometer
# romney romney thermometer
# kennedy robert kennedy thermometer
# muskie muskie thermometer
# agnew agnew thermometer
# lemay "bombs away with Curtis LeMay" thermometer
#
# Read Just The Thermometer Data From 1968 Survey
#
# Remove all objects just to be safe
#
rm(list=ls(all=TRUE))
library(MASS)
library(stats)
#
T <- matrix(scan("C:/ucsd_homework_6/therm68.txt",0),ncol=12,byrow=TRUE)
#
nrow <- length(T[,1])
ncol <- length(T[1,])
#
#
# Labels For Candidates
#
junk <- NULL
junk[1] <- "Wallace"
junk[2] <- "Humphrey"
junk[3] <- "Nixon"
junk[4] <- "McCarthy"
junk[5] <- "Reagan"
junk[6] <- "Rockefeller"
junk[7] <- "LBJ"
junk[8] <- "Romney"
junk[9] <- "Kennedy"
junk[10] <- "Muskie"
junk[11] <- "Agnew"
junk[12] <- "LeMay"
#
# The range of the 1968 Feeling Thermometers was 0 to 97 -- 98 and 99
# were used as missing values. You need to tell R that 98 and 99 are
# missing. To do this, use the following command:
#
# If T[i,j] = 98 or 99 set TT[i,j] = NA (missing data)
# else if set TT[i,j] = T[i,j]
#
TT <- ifelse(T==98 | T==99,NA,T)
#
# To compute the correlation matrix use the command below:
# The "pairwise.complete.obs" tells R to throw away missing
# data pair-wise, not list-wise (that is, the whole row of data!).
#
R <- cor(TT,use="pairwise.complete.obs")
RR <- R
#
#
# Transform the Correlation Matrix to Distance Matrix
#
i <- 0
while (i < ncol) {
i <- i + 1
j <- 0
while (j < ncol) {
j <- j + 1
#
# This is the Normal Transformation
#
RR[i,j] <- (1 - R[i,j])
#
#
}
}
#
# Call Classical Kruskal-Young-Shepard-Torgerson Non-Metric
# Multidimensional Scaling Program
#
# RR -- Input
# dim=2 -- number of dimensions
# y -- starting configuration (generated internally)
#
# Scale in two dimensions
#
kdim <- 2
y <- rep(0,kdim*ncol)
dim(y) <- c(ncol,kdim)
#
# Call Kruskal NonMetric MDS
#
wandrnmds <- isoMDS(RR,y=cmdscale(RR,kdim),kdim, maxit=50)
# as.dist transforms a square symmetric matrix of distances
RR.dist <- as.dist(RR,diag=FALSE,upper=FALSE) into a distance object. This is necessary for the Shepard(...) routine
shepardcheck.sh <- Shepard(RR.dist,wandrnmds$points) Shepard is an undocumented function in R
plot(shepardcheck.sh, type="n",asp=1,main="",xlab="",ylab="", I figured this out by trial and error!!
xlim=c(0,2),ylim=c(0,2),font=2) I copied the syntax from the bottom of the isoMDS page!!
points(shepardcheck.sh$x, shepardcheck.sh$y,pch=16,col="red") The key is to use the lower left triangle distance matrix from
# the as.dist function.
# The "S" means "stair-steps"
#
lines(shepardcheck.sh$x, shepardcheck.sh$yf,lty=1,lwd=2,type = "S",font=2)
#
# Main title
mtext("Shepard Diagram for MDS Solution\nWeisberg and Rusk",side=3,line=1.00,cex=1.2,font=2)
# x-axis title
mtext("Observed Dissimilarities",side=1,line=2.75,font=2,cex=1.2)
# y-axis title
mtext("Estimated Dissimilarities (D-hats)",side=2,line=2.75,font=2,cex=1.2)
#
#
# This creates another Graphics Device in R
#
windows()
xmax <- c(wandrnmds$points[,1],wandrnmds$points[,2])
axismax <- max(abs(xmax))
#
plot(wandrnmds$points[,1],wandrnmds$points[,2],type="n",asp=1,
main="",
xlab="",ylab="",
xlim=c(-axismax,axismax),ylim=c(-axismax,axismax),font=2)
#
# Main title
mtext("The 1968 Candidate Configuration\nFrom MDS Program in R",side=3,line=1.00,cex=1.2,font=2)
# x-axis title
mtext("Liberal - Conservative",side=1,line=2.75,font=2,cex=1.2)
# y-axis title
mtext("Anti-Wallace Wallace",side=2,line=2.75,font=2,cex=1.2)
#
#
# pos -- a position specifier for the text. Values of 1, 2, 3 and 4,
# respectively indicate positions below, to the left of, above and
# to the right of the specified coordinates
#
namepos <- NULL
namepos[1] <- 2 # Wallace
namepos[2] <- 3 # Humphrey
namepos[3] <- 4 # Nixon
namepos[4] <- 2 # McCarthy
namepos[5] <- 4 # Reagan
namepos[6] <- 2 # Rockefeller
namepos[7] <- 3 # LBJ
namepos[8] <- 2 # Romney
namepos[9] <- 4 # Kennedy
namepos[10] <- 2 # Muskie
namepos[11] <- 4 # Agnew
namepos[12] <- 2 # LeMay
#
text(wandrnmds$points[,1],wandrnmds$points[,2],junk,pos=namepos,offset=0.5,col="blue",font=2)
points(wandrnmds$points[,1],wandrnmds$points[,2],pch=16,col="red",font=2)
text(-0.7,1.0,paste("Stress = ",
0.01*round(wandrnmds$stress, 2)),col="purple",font=2)
#
# This creates another Graphics Device in R
#
windows()
#
# Create Data For Gradient of Generalization Plots
#
#
y <- rep(0,((ncol*(ncol-1))/2)*2)
dim(y) <- c(((ncol*(ncol-1))/2),2)
#
i <- 1
kk <- 0
while (i <= ncol) {
j <- i
while (j <= ncol) {
k <- 0
dist <- 0.0
while (k < kdim) {
k <- k+1
dist <- dist + (wandrnmds$points[i,k]-wandrnmds$points[j,k])^2
}
if(i != j) {
kk <- kk +1
y[kk,1] <- dist
y[kk,2] <- R[i,j]
# y[kk,2] <- RR[i,j]
}
j <- j + 1
}
i <- i + 1
}
#
#
ylow <- min(y[,2])
yhigh <- max(y[,2])
plot(y[,1],y[,2],ylim=c(ylow,yhigh),
xlab="",ylab="",col="red",font=2)
lines(lowess(y[,1],y[,2],f=.2),lwd=3)
text(10,80,"Line estimated \nUsing Lowess")
#
# Main title
mtext("Shepard's Theory of Generalization\nWeisberg and Rusk Data",side=3,line=1.00,cex=1.2,font=2)
# x-axis title
mtext("Psychological Distance",side=1,line=2.75,font=2,cex=1.2)
# y-axis title
mtext("Observed Similarity",side=2,line=2.75,font=2,cex=1.2)
#
#
# Save The Shepard Graph Data Sorted Ascending
#
kp <- order(y[,2])
shepard <- cbind(y[kp,1],y[kp,2])
#
-
Run Weisberg_and_Rusk_Shepard_Plot.r and you will get the following three graphs:
- Turn in these three graphs.
- We are now going to compare our results from R
with those from KYST. To do this, we need to get
the Pearson Correlation matrix stored in the matrix R out into a file that
we can then submit to KYST. At the command line in
R type:
write.matrix(R,"c:/ucsd_homework_6/R-table2.txt") -- write.matrix writes a matrix to a file nicely formatted
Bring the file up in Epsilon. It should look like this:

Type in the names of the 12 candidates so that your file looks like this:

Now, use Epsilon to stack the following commands on top of the correlation matrix:TORSCA PRE-ITERATIONS=3 DIMMAX=3,DIMMIN=1 PRINT HISTORY,PRINT DISTANCES COORDINATES=ROTATE ITERATIONS=50 REGRESSION=DESCENDING DATA,LOWERHALFMATRIX,DIAGONAL=PRESENT,CUTOFF=-2.00 1968 FEELING THERMOMETER CORRELATION MATRIX 12 1 1 (12X,12F12.8)
and do not forget to put COMPUTE and STOP on the bottom!
Report the Stress Values for 1, 2, and 3 dimensions and use R to graph the results in two dimensions.
- Use R to produce a Shepard Diagram
for the two dimensional solution in the same format as
Homework 2 question 1.
- Make a graph of the eigenvalues of the correlation matrix like the one you did for
Homework 5 question 2.e. Note that you can get the
eigenvalues by using the eigen(..) command in R.



and place them in the same folder on a WINTEL machine. Read the Aldrich-McKelvey scaling program page to see how to run the program.
Here are the first three lines of OLS68A.DAT.
1681 0 10 1 1 1 1 1 63 4 4 5 7 1 2 2 3 7 1 1
1124 0 10 1 0 0 0 1 82 1 1 4 4 1 1 1 1 4 1 5
78 5 10 1 0 1 1 1 78 2 1 5 7 4 5 5 6 6 7 5
The variables, in order, are:
RESPONDENT ID = unique 4 digit number
PARTY ID = 0 to 6 -- 0 = Strong Democrat
1 = Weak Democrat
2 = Lean Democrat
3 = Independent
4 = Lean Republican
5 = Weak Republican
6 = Strong Republican
RAW INCOME = **do not use**
FAMILY INCOME = income quintile 1 - 5
SEX = 0 Man, 1 Woman
RACE = 0 White, 1 Black
SOUTH = 0 North, 1 South
EDUCATION = 1 High School or less, 2 Some College, 3 College
AGE = In Years
URBAN UNREST SCALE = Johnson, Humphrey, Nixon, Wallace, Self-Placement
VIETNAM SCALE = Johnson, Humphrey, Nixon, Wallace, Self-Placement
VOTED = 1 Voted, 5 Did Not Vote
Run the Aldrich-McKelvey scaling procedure using both the urban unrest and
vietnam files. In particular, for the urban unrest scale here are the commands:MCKALNEW
Control Card File Name? URBAN68.CTL
Data File Name? OLS68A.DAT
Output File Name? URBAN.PRN
Coordinate Output File Name? URBAN.DAT
The program reads URBAN68.CTL and OLS68A.DAT and writes the output files to disk. The coordinates for the political stimuli are in URBAN.PRN. In particular, here is the relevant portion of URBAN.PRN:
etc etc etc
******************************************************************************
PERFORMANCE INDEX= 0
EIGENVALUES
-1070.0801
-936.8338
-251.0831
0.0012
******************************************************************************
******************************************************************************
STIMULUS COORDINATES
LBJ HHH NIXON WALLA
-0.3978 -0.4262 0.0116 0.8124 These are the coordinates
STIMULUS COORDINATES RAW DATA
-0.4087 -0.4229 0.0232 0.8084
******************************************************************************
CORRECTED GOODNESS OF FIT AND RAW FIT
0.0919 0.5075
etc etc etc
- Graph the scaled stimuli
coordinates against each other using R -- that is,
use the Vietnam coordinates as the horizontal axis and the Urban Unrest coordinates
as the vertical axis. Use the names of the candidates and label the graph and
the axes appropriately. Why do you think the plot looks the way it does?
- Use Epsilon to merge the party ID variable
from OLS68A.DAT into the coordinate output file. For example, here are the
first few lines of the coordinate output file for the urban unrest scale:
LINE # CASE # R POS ALPHA BETA SCALED POS RSQ 1 1681 1.0 -2.6243 0.5249 -2.0994 0.9994 0.9997 2 1124 1.0 -0.8831 0.3532 -0.5298 0.6790 0.8240 3 78 4.0 -0.9588 0.2557 0.0639 0.8992 0.9483 4 553 4.0 -1.2302 0.2895 -0.0724 0.6460 0.8037The second column is the respondent ID number. Use the respondent ID number to match OLS68A.DAT with the output file and insert the party ID code into the output file. After you have inserted the party code you can delete all the columns except the party code, BETA (you will need that for graphing), and the Scaled Position. If you have done everything correctly the first few lines of your file should look like this:0 0.5249 -2.0994 0 0.3532 -0.5298 5 0.2557 0.0639 1 0.2895 -0.0724 1 0.2763 0.6907 1 1.3930 -0.3482 0 1.0597 -0.5298 0 0.2322 -0.3482 0 0.4371 -0.8742 5 0.3901 0.6827 0 0.0033 0.0050 0 0.2119 -0.5298 1 0.2624 0.2624 2 0.2938 -0.5142 1 0.2745 0.1373 etc. etc. etc.Write an Epsilon text macro that inserts the party variable into the coordinate file. In the macro, use a split screen and place the coordinate file in the top screen and OLS68A.DAT in the bottom screen. When you begin it should look like this:

The beginning of the text macro should look like this:(define-macro "hw6" "C-U20C-F C-U5C-BC-KC-YC-DC-AC-X
Open up another window and put the above macro fragment in it and you should be here:C-Y C-U3C-F C-U4C-BC-KC-YC-DC-AC-X C-Y")

Finish constructing the macro and turn in the listing.
- Read the above file into R and
make smoothed histograms of the scaled positions of the respondents
by party ID. For example, to make smoothed histograms of the Strong Democrats
and Strong Republicans use this R Program:
 Smoothed_Histogram_hw_6_2006.r --
R Program to Plot Strong Democrats and Strong Republicans on Urban Unrest Scale
Smoothed_Histogram_hw_6_2006.r --
R Program to Plot Strong Democrats and Strong Republicans on Urban Unrest Scale
Here is what Smoothed_Histogram_hw_6_2006.r looks like:# # # Smoothed_Histogram_hw_6_2006.r -- Plots Strong Democrats and Strong Republicans on # 1968 Urban Unrest Scale # # rm(list=ls(all=TRUE)) # # library(MASS) # T <- matrix(scan("C:/UCSD_Homework_6/urban_hw6.txt",0),ncol=3,byrow=TRUE) # # Gore and Bush Voters # strong.democrat <- T[T[,1]==0 & T[,2] > 0,3] Select Strong Democrats With Positive Betas strong.republican <- T[T[,1]==6 & T[,2] > 0,3] Select Strong Republicans With Positive Betas # DemShare <- length(strong.democrat)/(length(strong.democrat)+length(strong.republican)) These two commands just compute RepShare <- length(strong.republican)/(length(strong.democrat)+length(strong.republican)) the proportions for the two Parties # demdens <- density(strong.democrat) density computes kernel density estimates. (Also see bandwidth.) demdens$y <- demdens$y*DemShare This is a trick so that the two densities.... # repdens <- density(strong.republican) repdens$y <- repdens$y*RepShare ...will add to 1.0 # ymax1 <- max(demdens$y) ymax2 <- max(repdens$y) ymax <- 1.1*max(ymax1,ymax2) # plot(demdens,main="", xlab="", ylab="", xlim=c(-1.5,1.5),ylim=c(0,ymax),font=2) lines(demdens,lwd=3,col="red") lines(repdens,lwd=3,col="blue") # text( .50,0.800,"Red = Strong Democrats",col="red",font=2,cex=1.2) text( .50,0.725,"Blue = Strong Republicans",col="blue",font=2,cex=1.2) # Main title mtext("Strong Party Identifiers\nFrom 1968 Urban Unrest 7-Point Scale",side=3,line=1.50,cex=1.2,font=2) # x-axis title mtext("Urban Unrest Scale Value",side=1,line=2.75,cex=1.2) # y-axis title mtext("Density",side=2,line=2.5,cex=1.2) # arrows(-.398, 0.06,-.398,0.0,length=0.1,lwd=3,col="red") text(-.308,.08,"LBJ",font=2) arrows(-.426, 0.06,-.426,0.0,length=0.1,lwd=3,col="red") text(-.516,.08,"HHH",font=2) arrows( .012, 0.13, .012,0.0,length=0.1,lwd=3,col="blue") text( .000,.16,"Nixon",font=2) arrows( .812, 0.13, .812,0.0,length=0.1,lwd=3,col="green") text( .812,.18,"Wallace",font=2) # # LBJ HHH NIXON WALLA # -0.3978 -0.4262 0.0116 0.8124Here is the graph it produces:

Turn in this plot.
- Similar to the above, make a graph for all Democrats (0,1,2) and all Republicans (4,5,6). Adjust the labeling
accordingly and make certain that everything is neatly presented.
- Similar to the above, make a graph for all Democrats (0,1,2) and all Republicans (4,5,6) for the
Vietnam scale. Adjust the labeling
accordingly and make certain that everything is neatly presented.
- Similar to the above, make a graph for all Democrats (0,1,2), all Republicans (4,5,6), and
Independents (4) for the Vietnam scale. Adjust the labeling
accordingly and make certain that everything is neatly presented. To do this note that you will
have to add code to compute IndShare and adjust everything so that the three smoothed histograms
add up to 1.
idno respondent id number partyid strength of party id -- 0 to 6 income raw income category incomeq income quintile -- 1 to 5 race 0 = white, 1 = black sex 0 = man, 1 = woman south 0 = north, 1 = south education 1=HS, 2=SC, 3=College age age in years uulbj lbj position urban unrest uuhhh humphrey pos urban unrest uunixon nixon position urban unrest uuwallace wallace pos urban unrest uuself self placement urban unrest vnmlbj lbj pos vietnam vnmhhh hhh pos vietnam vnmnixon nixon pos vietnam vnmwallace wallace pos vietnam vnmself self placement vietnam voted 1=voted, 5=did not vote votedfor who voted for -- 1 = humphrey, 2= nixon, 3=wallace wallace wallace therm humphrey humphrey thermometer nixon nixon thermometer mccarthy mccarthy thermometer reagan reagan thermometer rockefeller rockefeller thermometer lbj lbj thermometer romney romney thermometer kennedy robert kennedy thermometer muskie muskie thermometer agnew agnew thermometer lemay "bombs away with Curtis LeMay" thermometerThe control card file for the metric unfolding procedure is shown below. The first line has the name of the data file. The first number in the second line is the number of stimuli, the next two numbers are the minimum and maximum number of dimensions to estimate, and the "10" is the number of iterations.
The third line contains some "antique" options we will never use. The only numbers that matter on this line are the "4" which indicates the number of identifying characters to read off each line of the data file (e.g., the respondent id number), and the "2" at the end. This is the number of missing data codes which appear in the sixth line.
The first number in the fourth line is a tolerance value -- leave it as is. The next three numbers are parameters to transform the input data into squared distances. In this case, let amx=-.02, bmx=2.0, and cmx=2.0. The following equation transforms the thermometers into squared distances:
d2 = (amx*t+bmx)cmx
where t = input data. This formula takes a linear transformation of the input data to the power cmx. With amx = -.02, bmx = 2.0, and cmx = 2.0, this is equivalent to subtracting the thermometer score from 100, dividing by 50, and then squaring. This converts t from a 0-100 scale to a 4-0 scale. If the data, t, are distances, set amx = 1.0, bmx = 0.0, and cmx = 2.0. If the data are correlations, set amx = -1.0, bmx = 1.0, and cmx=2.0 or 1.0 if the correlations are initially regarded as unsquared or squared distances respectively.
The next value, "1.5", is the maximum absolute expected coordinate value on any dimension. It is used for plotting purposes. If the squared distances are confined to a 4-0 scale, xmax=1.5 is usually sufficient. The last two numbers, "0.0" and "100.0", are the minimum and maximum expected values of the input data. These are used to catch coding errors in the input data. Anything out of range is treated as missing data.
The fifth line is the format of the data file and the sixth line contains the missing data codes.
Finally, the last 12 lines are labels for the stimuli.
OLS68B.DAT
12 2 2 10 0 0
1 1 0 4 2
.001 -0.02 2.0 2.0 1.5 0.0 100.0
(1X,4A1,60X,12F3.0)
98 99
WALLACE
HUMPHREY
NIXON
MCCARTHY
REAGAN
ROCKEFELLER
LBJ
ROMNEY
R.KENNEDY
MUSKIE
AGNEW
LEMAY
- Run MLSMU6. It will produce an output
file called FORT.22. The first 20 lines look like this:
WALLACE 1.2646 0.5154 217.4823 0.5541 1242.0000 HUMPHREY -0.5559 0.3738 114.7892 0.6968 1252.0000 NIXON 0.1480 -0.5415 123.2209 0.5319 1250.0000 MCCARTHY -0.6251 -0.4938 151.8926 0.3854 1204.0000 REAGAN 0.3080 -0.8895 131.8091 0.4380 1212.0000 ROCKEFELLER -0.5579 -0.5995 148.1413 0.3724 1229.0000 LBJ -0.5223 0.4905 147.0334 0.5573 1253.0000 ROMNEY -0.4736 -0.7866 111.3147 0.3434 1167.0000 R.KENNEDY -0.4245 0.2351 148.8571 0.5418 1242.0000 MUSKIE -0.6611 0.1660 126.0836 0.4862 1177.0000 AGNEW 0.2341 -0.8706 114.1418 0.4675 1180.0000 LEMAY 1.1901 0.4267 174.3242 0.4601 1188.0000 1681 -0.0285 0.2555 0.7918 0.6824 12.0000 1124 -0.1768 0.2692 1.4788 0.6992 12.0000 78 0.5707 -0.1514 3.5611 0.2141 12.0000 553 0.1376 0.1064 0.1597 0.7047 9.0000 7 0.2542 0.1235 1.2634 0.0116 12.0000 412 0.2781 0.0867 0.1024 0.6197 12.0000 631 0.5017 0.1088 1.1196 0.0742 12.0000 1316 0.2175 -0.5842 1.1568 0.8577 12.0000 etc etc etc etc etc etcThe first two columns after the names are the two dimensional coordinates. The first 12 lines are the coordinates for the political candidates and lines 13 onward are the coordinates for the respondents. Use R to plot the 12 candidates in two dimensions. This plot should be very similar to the one you did for Question 1 above.
- Use Epsilon to insert the voted
and voted for variables into FORT.22 (strip off the candidate
coordinates first). Turn in the Epsilon macro
you used to do the insertion and the first 20 lines of the file.
- Use R to make two-dimensional plots
of the Voters, Non-Voters, Humphrey Voters only, Nixon Voters only, and
Wallace Voters only. For example, your Humphrey Voter plot should look
something like this:
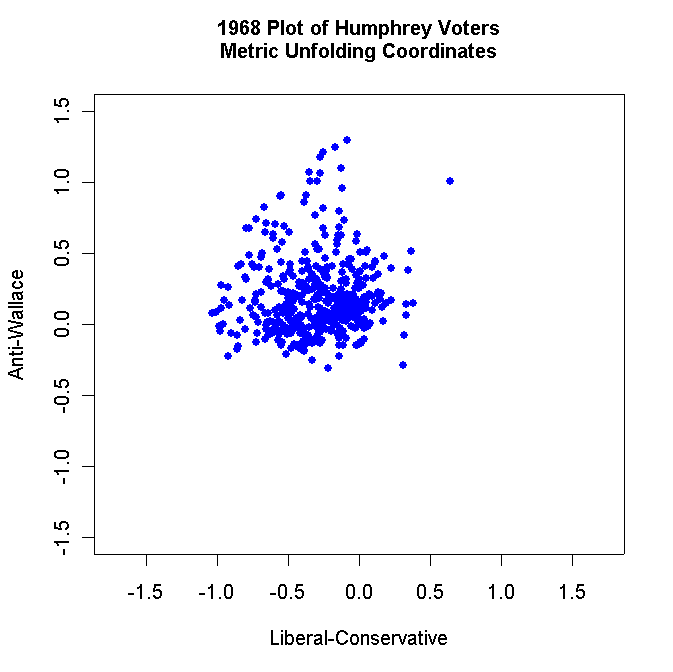
Label each plot appropriately and use solid dots to plot the respondents. Turn in all these plots.
Here are the first four lines of ELEC2000.DAT.
10787 4 8 0 0 0 2 49 1 0 65 60 30 40 70 50 998 998 40 59 75 63 65 6 1 3 6 4 0 2
21271 2 6 0 1 0 2 35 1 50 50 50 50 997 50 0 50 997 50 100 0 100 0 4 4 2 6 8 0 0
40285 2 6 0 0 0 2 63 0 70 55 55 60 65 55 55 65 50 60 70 65 65 90 6 5 5 5 5 0 1
50191 6 6 0 1 0 2 40 1 50 40 80 60 60 80 70 50 70 0 20 90 70 70 6 2 2 6 4 0 2
The variables, in order, are:
RESPONDENT ID = unique 8 digit number
PARTY ID = 0 to 6 -- 0 = Strong Democrat
1 = Weak Democrat
2 = Lean Democrat
3 = Independent
4 = Lean Republican
5 = Weak Republican
6 = Strong Republican
FAMILY INCOME = 1 to 22 - 1. A. NONE OR LESS THAN $4,999
2. B. $5,000-$9,999
3. C. $10,000-$14,999
4. D. $15,000-$24,999
5. E. $25,000-$34,999
6. F. $35,000-$49,999
7. G. $50,000-$64,999
8. H. $65,000-$74,999
9. J. $75,000-$84,999
10. K. $85,000-$94,999
11. M. $95,000-$104,999
12. N. $105,000-$114,999
13. P. $115,000-$124,999
14. Q. $125,000-$134,999
15. R. $135,000-$144,999
16. S. $145,000-$154,999
17. T. $155,000-$164,999
18. U. $165,000-$174,999
19. V. $175,000-$184,999
20. W. $185,000-$194,999
21. X. $195,000-$199,999
22. Y. $200,000 and over
RACE = 0 White, 1 Black
SEX = 0 Man, 1 Woman
SOUTH = 0 North, 1 South
EDUCATION = 1 High School or less, 2 Some College, 3 College
AGE = In Years
MARRIED = 0 Single, 1 Married
FEELING THERMOMETERS (0 TO 100)
= CLINTON
= GORE
= BUSH
= BUCHANAN
= NADER
= MCCAIN
= BRADLEY
= LIEBERMAN
= CHENEY
= HILLARY CLINTON
= DEMOCRATIC PARTY
= REPUBLICAN PARTY
= REFORM PARTY
= PARTIES IN GENERAL
LIBERAL-CONSERVATIVE SCALE (1=EXTREMELY LIBERAL, 2=LIBERAL, 3=SLIGHTLY LIBERAL,
4=MODERATE; MIDDLE OF THE ROAD, 5=SLIGHTLY CONSERVATIVE,
6=CONSERVATIVE, 7=EXTREMELY CONSERVATIVE)
= SELF-PLACEMENT
= CLINTON
= GORE
= BUSH
= BUCHANAN
PRE-POST INTERVIEW = 1 IF PRE-ELECTION INTERVIEW ONLY
VOTE CHOICE = 0 NON-VOTER
= 1 GORE
= 2 BUSH
= 3 3RD PARTY
MLSMU6 expects to read UNFOLD.CTL!! Consequently,
rename your current UNFOLD.CTL to UNFOLD_1968.CTL and then you can
copy UNFOLD_2000.CTL to UNFOLD.CTL.- Run MLSMU6. It will produce an output
file called FORT.22. The first 20 lines look
like this:
CLINTON -0.7879 -0.0317 153.1404 0.7198 1477.0000 GORE -0.7133 -0.1701 112.1776 0.7061 1468.0000 BUSH 0.8234 -0.2492 149.4325 0.5889 1458.0000 BUCHANAN 0.4576 1.0536 178.0645 0.3114 1246.0000 NADER -0.2737 0.7599 174.6307 0.2645 1094.0000 MCCAIN 0.2850 -0.6498 122.5794 0.3691 1182.0000 BRADLEY -0.0780 -0.7509 106.1498 0.3689 1088.0000 LIEBERMAN -0.3428 -0.6394 107.1314 0.4758 1096.0000 CHENEY 0.7002 -0.4687 107.9753 0.5099 1147.0000 HILLARY -0.8617 0.0625 203.7540 0.6459 1466.0000 DEMPARTY -0.6788 -0.1713 112.8208 0.6861 1453.0000 REPUBPARTY 0.8235 -0.3286 142.8395 0.5546 1447.0000 REFORMPTY 0.1644 1.0398 132.9094 0.3140 1128.0000 PARTIES 0.1949 -0.7946 158.0865 0.2290 1413.0000 1 0.3666 -0.0534 1.2943 0.3584 12.0000 2 -0.2740 0.6767 2.5447 0.5465 12.0000 4 0.0094 0.0645 0.8008 0.0000 14.0000 5 0.5073 -0.0010 1.3888 0.6249 14.0000 7 0.2719 0.0294 0.3600 0.5458 14.0000 8 -0.6582 -0.2931 1.8168 0.7683 14.0000 etc etc etc etc etc etcUse R to plot the 14 stimuli in two dimensions. This plot should be similar in format to the ones you did for the 1968 configuration above.
- Use Epsilon to insert the
VOTE CHOICE variable into FORT.22 (strip off the candidate
coordinates first). Turn in the Epsilon macro
you used to do the insertion and the first 20 lines of the file.
- Use R to make two-dimensional plots
of the Voters, Non-Voters, Gore Voters only, and
Bush Voters only. For example, your Gore Voter plot should look
something like this:
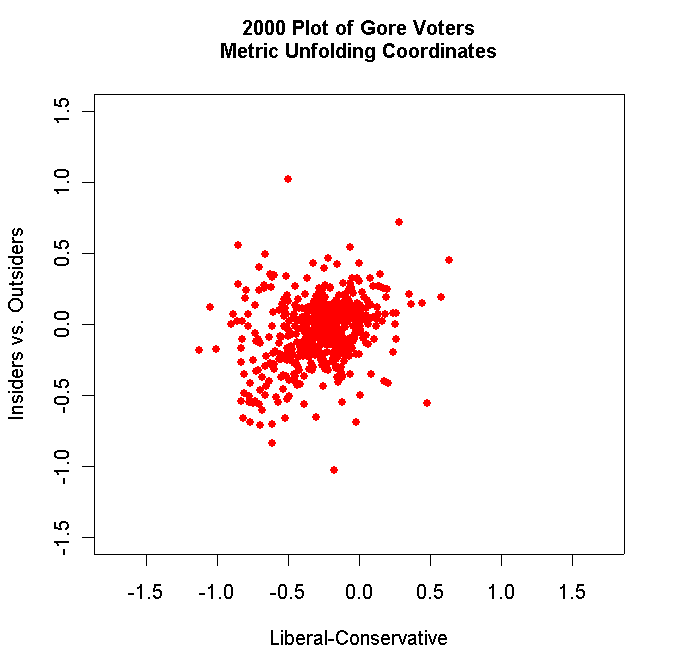
Label each plot appropriately and use solid dots to plot the respondents. Turn in all these plots.
- Use R to make smoothed histograms --
using the first dimension from the thermometer scaling --
of the Voters and Non-Voters only, and the Gore Voters, Bush Voters, and Non-Voters. For
example, your Bush-Gore-NonVoters plot should look
something like this:

Here is the trick for getting the percentage breakdown in the plot:# text(-1.0,0.53,paste("Gore Voters ", 100.0*round(goreShare, 3)),col="red",font=2) text(-1.0,0.5,paste("Bush Voters ", 100.0*round(bushShare, 3)),col="blue",font=2) text(-1.0,0.47,paste("Non Voters ", 100.0*round(nonShare, 3)),col="black",font=2) #Turn in the R code and the plots.
- Run W-NOMINATE on the 104th
House. Turn in the NOM21.DAT output file.
- The legislator coordinates are in the output file NOM31.DAT. The
first few lines should look similar to this:
11049990999 0USA 100 CLINTON 55 17 6 99 0.733 -0.587 0.065 21041509041 1ALABAMA 20000CALLAHAN 563 58 15 503 0.853 0.729 0.043 31042930041 2ALABAMA 20000EVERETT 571 70 21 502 0.825 0.746 0.041 41041563241 3ALABAMA 10000BROWDER 459 89 120 462 0.664 -0.037 0.015 51041100041 4ALABAMA 10000BEVILL 438 121 108 462 0.660 -0.081 0.015 61042910041 5ALABAMA 10000CRAMER 470 97 116 480 0.662 -0.023 0.014 71042930141 6ALABAMA 20000BACHUS 602 32 34 488 0.856 0.689 0.036 81042930241 7ALABAMA 10000HILLIARD 457 121 34 504 0.726 -0.643 0.023 91041406681 1ALASKA 20000YOUNG, DON 519 49 31 466 0.814 0.592 0.031 101042950061 1ARIZONA 20000SALMON 615 37 45 468 0.840 0.816 0.045 etc etc etc etc etc etcThe legislator coordinates are in the next to the last column (shown in red). For example, former President Clinton's coordinate is -0.587. Use R to make a smoothed histogram of the Republicans and Democrats in the 104th House using the estimated coordinates above (the party code is shown in blue). Use arrows to show the locations of former President Clinton and former Speaker of the House Newt Gingrich.
- Use Epsilon to change the number of
dimensions to "2" in NOMSTART.DAT and run the program again (be sure to
save NOM31.DAT from the one dimensional run as it will be overwritten).
NOMSTART.DAT (NOMSTART.H104) looks like this:
HOU104KH.ORD Name of Data File NOMINAL MULTIDIMENSIONAL UNFOLDING Title of Run 1321 1 5 Number RCs, Left on 1st, Up on 2nd 1 36 Number Dimensions, Number Characters to Read From Header 15.0000 0.5000 Starting Values for BETA and WEIGHT 0.0250 20 RC Min. Cutoff, Number RCs for Legislator (36A1,3600I1) Format for Roll Call File (1x,I4,36A1,1X,4i4,51f7.3) Format for Legislator Coordinate File -- NOM31.DAT (1x,I4,36A1,1X,51f7.3) Format for H-S Coordinate File -- FORT.34The red "1" in the fourth line is the number of dimensions. This is the number you should change to "2". Leave everything else in the file the same! Run W-NOMINATE on the 104th House in two dimensions. Turn in the NOM21.DAT output file.
- The two-dimensional coordinate file looks like this:
11049990999 0USA 100 CLINTON 54 17 7 99 0.729 -0.594 -0.116 0.066 0.129 21041509041 1ALABAMA 20000CALLAHAN 561 36 17 525 0.880 0.758 0.653 0.042 0.132 31042930041 2ALABAMA 20000EVERETT 569 50 23 522 0.852 0.774 0.634 0.040 0.132 41041563241 3ALABAMA 10000BROWDER 473 35 106 516 0.733 -0.034 0.842 0.015 0.083 51041100041 4ALABAMA 10000BEVILL 448 57 98 526 0.723 -0.079 0.759 0.015 0.075 61042910041 5ALABAMA 10000CRAMER 474 46 112 531 0.710 -0.018 0.688 0.015 0.064 71042930141 6ALABAMA 20000BACHUS 597 25 39 495 0.861 0.695 0.232 0.035 0.078 81042930241 7ALABAMA 10000HILLIARD 445 117 46 508 0.748 -0.642 0.417 0.023 0.046 91041406681 1ALASKA 20000YOUNG, DON 517 34 33 481 0.839 0.600 0.583 0.031 0.122 101042950061 1ARIZONA 20000SALMON 623 35 37 470 0.842 0.826 -0.119 0.045 0.075 etc etc etc etc etc etcThe legislator coordinates are are the third and fourth columns from the end (shown in red). For example, former President Clinton's coordinates are -0.594 and -0.116. Use R to plot the legislators in two dimensions. Use "D" for Non-Southern Democrats, "S" for Southern Democrats, "R" for Republicans, and "P" for President Clinton. This graph should be in the same format as the one you did for question 2.f of Homework 5.
- Run W-NOMINATE on the 104th
Senate. Turn in the NOM21.DAT output file.
- Use R to make a smoothed histogram
of the Republicans and Democrats in the 104th Senate using the estimated
coordinates from the NOM31.DAT file. Use arrows to show the
locations of former President Clinton, and Senators Kennedy and Helms.
- Use Epsilon to change the number of
dimensions to "2" in NOMSTART.DAT and run the program again (be sure to
save NOM31.DAT from the one dimensional run as it will be overwritten).
Use R to plot the legislators in two dimensions. Use
"D" for Non-Southern Democrats, "S" for Southern Democrats, "R" for Republicans, and
"P" for President Clinton. This graph should be in the same format as the one
you did for question 2.f of Homework 5.