# The "#" is a comment statement --
# double_center.r -- Double-Center Program that is, it tells the R compiler
# that what follows on this line are
# The Data Are assumed to be Squared Distances -- Data Must comments, not commands!
# Be Transformed to Squared Distances Below
#
T <- matrix(scan("D:/R_Files/colors.txt",0),ncol=14,byrow=TRUE) This reads in the Color Matrix Data -- Note that you have to tell it how many columns!
colornames <- read.csv("D:/R_Files/color_coords.txt",header=T,row.names=1) Same as Homework 4
attach(colornames) Same as Homework 4
TT <- T Copy matrix T into matrix TT
nrow <- length(T[,1]) Counts number of rows
ncol <- length(T[1,]) Counts number of columns
xrow <- NULL Initializes Vector
xcol <- NULL Initializes Vector
matrixmean <- 0 Initialize to zero
#
# Transform the Matrix This transforms the similarities data from a range of
# 0 - 100 to a range of 0 - 4 in squared distances
i <- 0
while (i < nrow) { Note that this loops nrow times because it starts at 0!
i <- i + 1 Increment the counter or it will loop forever!
j <- 0 Initialize column index to 0
while (j < ncol) { Note that this loops ncol times because it starts at 0!
j <- j + 1 Increment the counter or it will loop forever!
TT[i,j] <- ((100 - T[i,j])/50)**2 Here is the Transformation
}
}
T <- TT Copy matrix TT into matrix T
#
# Set Row and Column Vectors to zero
i <- 0 These two loops simply initialize the vectors to zero
while (i < nrow) {
i <- i + 1
xrow[i] <- 0.0
}
i <- 0
while (i < ncol) {
i <- i + 1
xcol[i] <- 0.0
}
# Compute Row Means and Matrix Mean -- Set TT(,) to Zeroes
i <- 0 Set counter to zero
while (i < nrow) { Loop over Rows
i <- i + 1 Increment the counter or it will loop forever
j <- 0 Set column counter to zero
while (j < ncol) { Loop over Columns to get Row Means
j <- j + 1 Increment the counter or it will loop forever
xrow[i] <- xrow[i]+T[i,j]/ncol Add up elements in the row (add across columns)
matrixmean <- matrixmean + T[i,j]/(nrow*ncol) This gives us the matrix mean
TT[i,j] <- 0 Initialize matrix TT to zero
}
}
# Compute Column Means
j <- 0 Set counter to zero
while (j < ncol) { Loop over Columns
j <- j + 1 Increment the counter or it will loop forever
i <- 0 Set row counter to zero
while (i < nrow) { Loop over Rows to get Column Means
i <- i + 1 Increment the counter or it will loop forever
xcol[j] <- xcol[j]+T[i,j]/nrow Add up elements in the column (add across rows)
}
}
# Double-Center the Matrix This Double-Centers the Matrix
i <- 0 Set counter to zero
while (i < nrow) { Loop over Rows
i <- i + 1 Increment the counter or it will loop forever
j <- 0 Set column counter to zero
while (j < ncol) { Loop over Columns
j <- j + 1 Increment the counter or it will loop forever
TT[i,j] <- (T[i,j]-xrow[i]-xcol[j]+matrixmean)/(-2) TT is the Double-Centered Matrix
}
} End of Double-Center Code
ev <- eigen(TT) Compute the Eigenvalues and Eigenvectors
DIMNEW.1 <- ev$vec[,1] Put the First Eigenvector in DIMNEW.1
DIMNEW.2 <- ev$vec[,2] Put the Second Eigenvector in DIMNEW.2
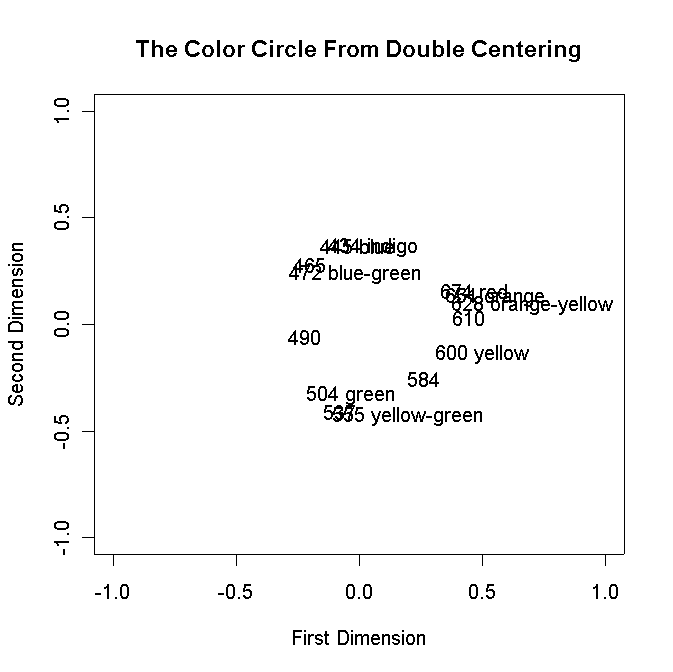
plot(DIMNEW.1,DIMNEW.2,type="n",main="The Color Circle From Double Centering",
xlab="First Dimension",ylab="Second Dimension",
xlim=c(-1.0,1.0),ylim=c(-1.0,1.0)) Plot Commands
text(DIMNEW.1,DIMNEW.2,labels=row.names(colornames),adj=0)
Download the R
program and two example files below and place them in the same directory
on your disk. Note that you will have to use Epsilon
to change the path statements in double_center.r.
R Program to Perform Double-Centering
Ekman Color Similarities Matrix
Color Coordinates
With Row Names Used in Homework 4Run double_center.r and you should see:
-
Turn in the Graph.
In R type:
eigenvalue <- abs(ev$val)
eigenvalue
and you should see:
[1] 7.928536e+00 5.197332e+00 1.763696e+00 1.495726e+00 6.338461e-01 [6] 4.120299e-01 1.660689e-01 1.266656e-01 7.386280e-02 1.666023e-02 [11] 5.380350e-03 9.296853e-15 1.069314e-01 1.897294e-01These are the eigenvalues of the double-centered matrix (technically, the absolute values of the eigenvalues). Paste these into Excel and make a plot like that shown in Home Work Number 3, problem 2.b. Turn in this plot with the appropriate title (e.g., "Eigenvalues of Double-Centered Color Data").
We are going to test Shepard's Universal Law by assuming that the color data are actually generated by an exponential loss function. To do this:
-
Make a copy of double_center.r --
double_center_2.r.
Bring double_center_2.r up in Epsilon.
Change the line "TT <- T" that comes right after the line "attach(colornames)" to:
TT <- ifelse(T <= 5,5,T) If T[i,j] £ 5 set T[i,j] = 5,
else if T[i,j] > 5 leave as is (replace with itself)
Right below this line insert the line:T <- TT
These two commands replace any entries in "colors.txt" that are less than 5 with 5 because the natural log of zero is negative infinity!
Replace the line "TT[i,j] <- ((100 - T[i,j])/50)**2" with:
TT[i,j] <- ((-1.0)*log(T[i,j]/100))**2
Repeat parts (a) and (b) with the plots appropriately titled.
1968 Election DataThe 1968 Election Data file contains some variables besides the thermometer scores that we will use in future homeworks. The variables are:
idno respondent id number partyid strength of party id -- 0 to 6 income raw income category incomeq income quintile -- 1 to 5 race 0 = white, 1 = black sex 0 = man, 1 = woman south 0 = north, 1 = south education 1=HS, 2=SC, 3=College age age in years uulbj lbj position urban unrest uuhhh humphrey pos urban unrest uunixon nixon position urban unrest uuwallace wallace pos urban unrest uuself self placement urban unrest vnmlbj lbj pos vietnam vnmhhh hhh pos vietnam vnmnixon nixon pos vietnam vnmwallace wallace pos vietnam vnmself self placement vietnam voted 1=voted, 5=did not vote votedfor who voted for -- 1 = humphrey, 2= nixon, 3=wallace wallace wallace therm humphrey humphrey thermometer nixon nixon thermometer mccarthy mccarthy thermometer reagan reagan thermometer rockefeller rockefeller thermometer lbj lbj thermometer romney romney thermometer kennedy robert kennedy thermometer muskie muskie thermometer agnew agnew thermometer lemay "bombs away with Curtis LeMay" thermometer
-
Make a copy of OLS68B.DAT -- therm68.txt -- and
use Epsilon to remove all the variables
except the 12 Thermometer Scores. Turn in the
Epsilon macro you used to create
therm68.txt.
Read the data into R with the command (be sure you use the appropriate path statement!):
T <- matrix(scan("D:/R_Files/therm68.txt",0),ncol=12,byrow=TRUE)
The range of the 1968 Feeling Thermometers was 0 to 97 -- 98 and 99 were used as missing values. You need to tell R that 98 and 99 are missing. To do this, use the following command:
TT <- ifelse(T==98 | T==99,NA,T) If T[i,j] = 98 or 99 set TT[i,j] = NA (missing data)
else if set TT[i,j] = T[i,j]
To compute the correlation matrix use the command:R <- cor(TT,use="pairwise.complete.obs")
The "pairwise.complete.obs" tells R to throw away missing data pair-wise, not list-wise (that is, the whole row of data!). Now type:
R
and you should something like this:
[,1] [,2] [,3] ....etc
[1,] 1.00000000 -0.3108400 0.01690949 ....etc
.... etc etc etc ...
You need this correlation matrix to duplicate what Weisberg and Rusk did with
KYST. Use
Epsilon to copy the correlation matrix into
your KYST control card file. Note that you will
have to reassemble the matrix using Epsilon and
note that because of the pecularities of R, the
second column of the matrix has one less digit than the other columns!!!
You will have to stick a zero at the end of each correlation in the second column to
get everything to work. Your KYST control card file
should look something like this:TORSCA PRE-ITERATIONS=3 DIMMAX=3,DIMMIN=1 PRINT HISTORY,PRINT DISTANCES COORDINATES=ROTATE ITERATIONS=50 REGRESSION=DESCENDING DATA,LOWERHALFMATRIX,DIAGONAL=PRESENT,CUTOFF=-2.00 1968 FEELING THERMOMETER CORRELATION MATRIX 12 1 1 (14X,12F12.8) Wallace 1.00000000 -0.31084000 0.01690949 ... etc etc ...etc etc ... COMPUTE STOPReport the Stress Values for 1, 2, and 3 dimensions and use R to graph the results in two dimensions.
Produce a Shepard Diagram for the two dimensional solution (the horizontal axis is the actual correlation data -- "DATA" in the KYST output file -- and the vertical axis is the estimated distances -- the "DIST" column in the KYST output file).
Make a plot of the first two eigenvectors of the correlation matrix using R (see problem 1 for how to do this -- be certain everything is properly labeled!).
Make a plot of the eigenvalues of the correlation matrix (see problem 1).
In R create the following 12 by 12 matrices (the t(ev$vec) is the transposed 12 by 12 matrix of eigenvectors and the symbol "%*%" is the matrix multiplication command):
hello <- diag(12)
ZZ <- t(ev$vec) %*% ev$vec
Are these two matrices -- hello and ZZ -- the same?
In R create the following matrices:
diag(hello) <- ev$val
RWORK <- ev$vec %*% hello %*% t(ev$vec)
What is RWORK? Be Specific!
Morse Code Data in Unfolding Format-
Run KYST and note that you will end up with
72 points! Point number 1 is "A" and point number
37 is also "A"! (Ignore the tokens in KYST!! They
will be off on this problem because there is no "0" -- zero!) Graph the
72 points with the appropriate labels and appropriate titles in
R.
Produce a Shepard Diagram for the two dimensional solution (the horizontal axis is the actual correlation data -- "DATA" in the KYST output file -- and the vertical axis is the estimated distances -- the "DIST" column in the KYST output file).