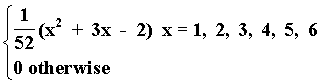
LEGACY CONTENT. If you are looking for Voteview.com, PLEASE CLICK HERE

This site is an archived version of Voteview.com archived from University of Georgia on May 23, 2017. This point-in-time capture includes all files publicly linked on Voteview.com at that time. We provide access to this content as a service to ensure that past users of Voteview.com have access to historical files. This content will remain online until at least January 1st, 2018. UCLA provides no warranty or guarantee of access to these files.

Probability and Statistics                      Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Practice Midterm
Keith Poole

(10 Points)

1. You roll one dice three times. If it is known that a 1 appeared at least once in the three rolls, what is the probability that a 1 appeared only once?

P(Y = 1 | Y ³ 1) = P(Y = 1)/P(Y ³ 1) = P(Y = 1)/[1 - P(Y = 0)]
Clearly P(Y = 0) = (5/6)3 and
P(Y = 1) = 3(1/6)(5/6)(5/6)
because you have to take into account the three possibilities for the "1" to appear. Hence

P(Y = 1 | Y ³ 1) = [3(1/6)(5/6)(5/6)]/[1 - (5/6)3]

Probability and Statistics                      Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Practice Midterm
Keith Poole

(10 Points)

2. We have 3 urns. One contains 5 red balls, 3 white, and 2 blue. A second urn contains 4 red, 4 white, and 2 blue. And the third urn contains 1 red, 7 white, and 2 blue. What is the probability that the three balls are the same color.

P(All three balls the same color) = P(three Red) + P(three White) + P(three Blue) =
(5/10)(4/10)(1/10) + (3/10)(4/10)(7/10) + (2/10)(2/10)(2/10) =
(20 + 84 + 8)/1000 = .112

Probability and Statistics                      Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Practice Midterm
Keith Poole

(10 Points)

3. Suppose we have the distribution function:

 

F(x) =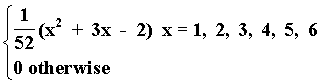

Find the corresponding discrete probability distribution, f(x).

Note that I incorrectly specified F(x). I should have said something like: "Suppose the following formula gives the correct F(x) values corresponding to the values of a discrete random variable. Find the corresponding discrete probability distribution."
To properly define F(x), I would have to specify the values between the integer values of x! And I left out that F(x) = 1 when x > 6.
In any event, note that: F(0) = 0, F(1) = 2/52, F(2) = 8/52, F(3) = 16/52, F(4) = 26/52, F(5) = 38/52, and F(6) = 1
Now, since f(x) = F(x) - F(x - 1), we get

                          {   2/52  x = 1  
                          {
                          {   6/52  x = 2 
                          {
                          {   8/52  x = 3  
                          {
                   f(x) = {  10/52  x = 4  
                          {
                          {  12/52  x = 5  
                          {
                          {  14/52  x = 6  
                          {
                          {  0 otherwise

Probability and Statistics                      Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Practice Midterm
Keith Poole

(10 Points)

4. Suppose we have a continuous probability distribution

f(x) =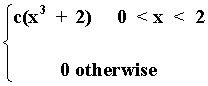

a. Find c.

ò02 c(x3 + 2)dx = c(x4/4 + 2x)|02 = c(16/4 + 4) = 8c; hence, c = 1/8

b. Find E(X).

E(X) = ò0 2 xf(x)dx = ò02 {[x(x3 + 2)]/8}dx = (1/8)(x5/5 + 2x2/2)|02 = (1/8)(32/5 + 4) = 1.3

c. Find VAR(X).

E(X2) = ò0 2 x2f(x)dx = ò02 {[x2(x3 + 2)]/8}dx = (1/8)(x6/6 + 2x3/3)|02 = (1/8)(64/6 + 16/3) = 2
Hence, VAR(X) = E(X2) - [E(X)]2 = 2 - 1.32 = 0.31

Probability and Statistics                      Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Practice Midterm
Keith Poole

(10 Points)

5. Suppose we have a discrete bivariate probability distribution

f(x,y) =

Find VAR(X) and VAR(Y)

                               y

                           1   2   3
                         ------------
                       1 | 3   2   1 | 6
                         |           |
                    x  2 | 7   6   5 |18
                         |           |
                       3 |11  10   9 |30
                         |           |
                         ---------------
                          21  18  15 |54

E(X) = åi=1,3 åj=1,3 xif(xi, yj) = åi=1,3 xif1(xi) = 1(6/54) + 2(18/54) + 3(30/54) = 132/54
E(X2) = 1(6/54) + 4(18/54) + 9(30/54) = 348/54
E(Y) = 1(21/54) + 2(18/54) + 3(15/54) = 102/54
E(Y2) = 1(21/54) + 4(18/54) + 9(15/54) = 228/54
VAR(X) = 348/54 - (132/54)2
VAR(Y) = 228/54 - (102/54)2

Probability and Statistics                      Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Practice Midterm
Keith Poole

(10 Points)

6. Suppose we have two groups of people. In the first group there are 9 women and 10 men and in the second group there are 13 women and 5 men. Suppose a person is randomly selected from each group. Let Y = 1 if the two persons are the same sex, and let Y = 0 if the two persons are not the same sex. What is the probability distribution of Y?

P(Y = 0) = P(Man Group I Ç Woman Group II) + P(Woman Group I Ç Man Group II) = (10/19)(13/18) + (9/19)(5/18) = .5117
P(Y = 1) = P(Man Group I Ç Man Group II) + P(Woman Group I Ç Woman Group II) = (10/19)(5/18) + (9/19)(13/18) = .4883
Hence 
                           { .5117 y = 0                    
                           {                                 
                    f(y) = { .4883 y = 1                 
                           {                               
                           {  0 otherwise

Probability and Statistics                      Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Practice Midterm
Keith Poole

(10 Points)

7. A woman fires 10 shots at a target. The probability is .9 that she will hit the target on any given shot. The shots are independent of one another. What is the probability that she has hit the target at least twice if it is known that she has hit the target at least once.

Note that this is a binomial distribution with parameters p = .9 and n = 10.
P(Y ³ 2 | Y ³ 1) = P(Y ³ 2)/P(Y ³ 1) = [1 - P(Y £ 1)]/[1 - P(Y = 0)] =
[1 - .110 - (10 choose 1).91.19]/ [1 - .110]

Probability and Statistics                      Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Practice Midterm
Keith Poole

(10 Points)

8. Suppose we have the continuous function

f(x) =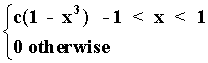

 

Does a c exist such that this is a probability distribution.

ò-11 c(1 - x3)dx = c(x - x4/4)|-11 = c(1 - 1/4 + 1 + 1/4) = 2c; hence, c = 1/2

Now, since f(x) ³ 0 for all values of x when c = 1/2, f(x) is indeed a probability distribution.

Probability and Statistics                      Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Practice Midterm
Keith Poole

(10 Points)

9. Suppose we have 100 executives and we have to form 4 committees of 37, 23, 15, and 10 people, respectively. How many ways can the committees be selected.

This is the Multinominal Coefficient:

(100 choose 37 23 15 10 15) = 100!/37!23!15!10!15!

Probability and Statistics                      Name__________________________
Spring 1998 Flex-Mode and Flex-Time 45-733
Practice Midterm
Keith Poole

(10 Points)

10. Suppose we have the bivariate continuous probability distribution

f(x,y) =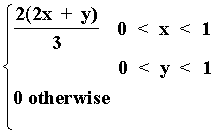

Find P(X > 1/2 Ç Y < 1/2)


P(X > 1/2 Ç Y < 1/2) = P(X > 1/2, Y < 1/2] = ò1/21 ò01/2 (2/3)(2x + y)dydx =
(2/3)ò1/21 [(2xy + y2/2)|01/2]dx = (2/3)ò1/21 (x + 1/8)dx =
(2/3)[(x2/2 + x/8)|1/21] = (2/3)(1/2 + 1/8 - 1/8 - 1/16) = 7/24