P[-.02 <
F [+(0.2/9)n1/2 ] - F [-(0.2/9)n1/2 ] = 2F [(0.2/9)n1/2 ] - 1 ³ 0.95
Þ F [(0.2/9)n1/2 ] ³ 0.975
So (0.2/9)n1/2 ³ 1.96
n ³ 7780
Probability and Statistics
Name__________________________
Spring 1997 Flex-Mode 45-733
Practice Final
Keith Poole
(10 Points)
1. Suppose we take a random sample of size n from a normal distribution with mean m and variance 81. Determine the minimum sample size, n, such that the absolute difference between the sample mean and m is less than .2 with probability at least .95.
P[ |![]() -
m
| < 0.2] ³
0.95
-
m
| < 0.2] ³
0.95
P[-.02 < ![]() -
m
< 0.2} = P[ -(0.2/9)n1/2<
(
-
m
< 0.2} = P[ -(0.2/9)n1/2<
(![]() -
m)n1/2/9<(0.2/9)n1/2]
=
-
m)n1/2/9<(0.2/9)n1/2]
=
F
[+(0.2/9)n1/2 ] - F
[-(0.2/9)n1/2 ] =
2F
[(0.2/9)n1/2 ] - 1 ³
0.95
Þ
F
[(0.2/9)n1/2 ] ³
0.975
So (0.2/9)n1/2 ³
1.96
n ³
7780
Probability and Statistics
Name__________________________
Spring 1997 Flex-Mode 45-733
Practice Final Exam
Keith Poole
(10 Points)
2. A random sample of 101 is drawn from a normal distribution and
it is found that
![]() = 887
= 887
Construct 95% and 99% confidence limits for
s2.
![]()
for 95% limits a = 0.05, a/2 = 0.025, df = 100
C1 = 74.2219, C2 = 129.561
Þ (887/129.561) and (887/74.2219) = (6.846, 11.951)
For 99% limits a = 0.1, a/2 = 0.005, df = 100
C1 = 67.3276, C2 = 140.169
Þ (887/140.169) and (887/67.3276) = (6.328, 13.174)
Probability and Statistics
Name__________________________
Spring 1997 Flex-Mode 45-733
Practice Final Exam
Keith Poole
(10 Points)
3. Pitt and GSIA students independently take an identical Prob-Stat I midterm examination. Assume the scores in both populations are normally distributed. You draw a sample of 8 GSIA students and obtain the scores: 72, 95, 83, 80, 95, 83, 80, 90; and you draw a sample of 9 Pitt students and obtain the scores: 74, 94, 88, 78, 60, 71, 66, 90, 83. Test the null hypothesis that the variances of the two populations are the same against the alternative hypothesis that the variances are not the same (a = .01).
GSIA Pitt
N = 8 M = 9
![]() = 84.75
= 84.75
![]() = 78.22
= 78.22
S12 = 64.5
S22 = 132.19
H0:s
2g = s
2pitt
H1: s
2g¹
s
2pitt
Reject if 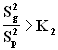 or
or 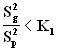
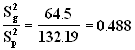
K2 = 7.69
K1 = 1/(8.68)=0.1152
Since 0.1152 < 0.488 < 7.69
DO NOT REJECT H0
Probability and Statistics
Name__________________________
Spring 1997 Flex-Mode 45-733
Practice Final Exam
Keith Poole
(10 Points)
4. Suppose you draw a random sample of size 13 from the CMU faculty and
find that the average age is 49 years with sample standard deviation of 15
years. Assume that age is normally distributed. Construct the best possible
decision rule for the hypothesis test:
H0: m = 56
H1: m
¹ 56
Do you accept or reject the null hypothesis
(a = .05).
Reject if ![]() or
or ![]()
a/2 = 0.025, 12df,
t.025 = 2.179
![]()
Since -2.179<-1.683<2.179
DO NOT REJECT H0
Probability and Statistics
Name__________________________
Spring 1997 Flex-Mode 45-733
Practice Final Exam
Keith Poole
(5 Points)
5. Suppose that the proportion of defective resistors in a large shipment to our plant is known to be .008. We take a random sample of 1000 resistors. What is the probability that less than 5 are defective.
l =np= (1000)(.008)=8
P(X<5)=F(4)=0.1
Probability and Statistics
Name__________________________
Spring 1997 Flex-Mode 45-733
Practice Final Exam
Keith Poole
(10 Points)
6. Suppose we have the continuous probability distribution
f(x) = 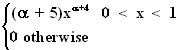
Find the maximum likelihood estimator for a .
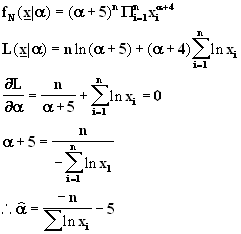
Probability and Statistics
Name__________________________
Spring 1997 Flex-Mode 45-733
Practice Final Exam
Keith Poole
(10 Points)
7. Suppose you draw a random sample of 8 first year masters students and find that their ages are 24, 29, 31, 29, 28, 28, 26, 32, respectively; and you draw a random sample of 6 second year masters students and find that their ages are 33, 31, 26, 27, 28, 30, respectively. Assume age is normally distributed in both populations with equal variance. Construct 95% confidence limits for the difference in mean ages of first and second year masters students.
1st : N=8, ![]() =28.375, S12=6.554
=28.375, S12=6.554
2nd: M=6, ![]() =29.167, S22=6.697
=29.167, S22=6.697
a =0.5, t.025=2.179, 12df
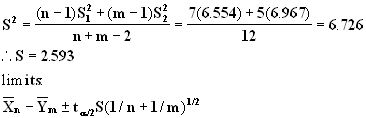
So (28.375-29.267)± (2.179)(2.593)(1/8+1/6)1/2
(-3.843, 2.259)
Probability and Statistics
Name__________________________
Spring 1997 Flex-Mode 45-733
Practice Final Exam
Keith Poole
(10 Points)
8. Suppose we have the bivariate continuous probability function
f(x,y) = 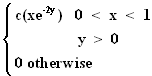
a. Find c.
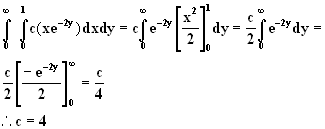
b. Are X, Y independent.
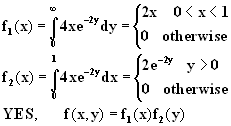
Probability and Statistics
Name__________________________
Spring 1997 Flex-Mode 45-733
Practice Final Exam
Keith Poole
(10 Points)
9. Suppose we know that exactly one of the following hypotheses must be true:
H0: s 2 = 350The population is normally distributed and the sample size is 30. How large must the sample variance be for you to reject the null hypothesis with a = .05.
Reject if (n-1)s2/s 02 > C2Probability and Statistics
Name__________________________
Spring 1997 Flex-Mode 45-733
Practice Final Exam
Keith Poole
(10 Points)
10. A manufacturer of a machine to fill paint cans claims that her machine will fill paint cans at a given weight with a standard deviation of .7 ounce. You take a random sample of 14 filled paint cans and find that s = .88. Perform the following hypothesis test:
H0: s 2 = .49Assume that the measurements are normally distribution and use a = .05.
Reject if (n-1)s2/s 02 > C2 or (n-1)s2/s 02 < C1
a = 0.05, C1 = 5.00874, C2 = 24.7356, 13dfHence (n-1)s2/s 02 = 13(0.88)(0.88)/(0.49)=20.545
Since 5.00874 < 20.545 < 24.7356
DO NOT REJECT
Probability and Statistics
Name__________________________
Spring 1997 Flex-Mode 45-733
Practice Final Exam
Keith Poole
(10 Points)
11. Suppose that the number of cars arriving at a drive through bank machine is governed by a Poisson process with a mean of 3 cars every 5 minutes. What is the probability that no more than 4 cars will arrive in a 5 minute period.
l =3, X = Number of Cars ,
P[X£ 4] = F(4) = 0.815
Probability and Statistics
Name__________________________
Spring 1997 Flex-Mode 45-733
Practice Final Exam
Keith Poole
(10 Points)
12. The waiting times for customers at a local store are independent random variables with a mean of 3.0 minutes and a standard deviation of 2.0 minutes. Use the Central Limit Theorem to find the approximate probability that 100 customers can be served in less than 4 hours 30 minutes at this store.
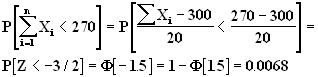
Probability and Statistics
Name__________________________
Spring 1997 Flex-Mode 45-733
Practice Final Exam
Keith Poole
(10 Points)
13. Suppose we have an urn containing 1000 balls numbered from 000 to 999. Six balls are drawn one at a time from the urn with replacement; that is, a ball is drawn, its numbered noted, and it is placed back in the urn. What is the probability that exactly two of the six numbers are the same and the other four are different.
![]()
Probability and Statistics
Name__________________________
Spring 1997 Flex-Mode 45-733
Practice Final Exam
Keith Poole
(10 Points)
14. A large shipment of memory chips is delivered to our computer manufacturing plant. We take a random sample of 100 chips and find that 8 are defective. Compute 95% confidence limits for p, the true proportion of defectives.
Central Limit Theorem, 1 - a = 0.95, a/2 = 0.025, Z0.025 = 1.96 p ± 1.96 (.08*0.92/100)1/2Probability and Statistics
Name__________________________
Spring 1997 Flex-Mode 45-733
Practice Final Exam
Keith Poole
(10 Points)
15. Seventeen capacitors were randomly selected from the output of a process supposedly producing 10-picofarad capacitors. The 17 capacitors actually showed a sample mean of 9.9 picofarads and a sample standard deviation of .3 picofarads. Find 95% and 99% confidence limits for the true capacitance of the capacitors produced by this process. Assume that the measurements are normally distributed.
![]()
![]()