45-733 PROBABILITY AND STATISTICS I Topic #1B

25 January 2000

Independent Events and Conditional Probability

1. Definition: Two events, A and B, are independent if and only if :
   P(A Ç B) = P(A)P(B).
   
   
2. Example 2.15 p47
   A = {1, 3, 5,}; B = {2, 4, 6}; C = {1, 2}
   P(A Ç B) = 0 < P(A)P(B) = 1/2 x 1/2 = 1/4
   P(A Ç C) = 1/6 = P(A)P(C) = 1/2 x 1/3 = 1/6
   P(B Ç C) = 1/6 = P(B)P(C) = 1/2 x 1/3 = 1/6
   So A and C are independent events and B and C are independent events, but A and B are not independent events.
   
   
3. Circuit Example
   Consider the following circuit of 5 identical relays. The probability that any relay works is .8 and the failures of the relays are independent. What is the probability that, when current is applied, it flows from point 1 to point 2?

   
   
                             -----B-----
                             |         |
                       1---A--         --E---2
                             |         |
                             ---C---D---
   

   Note that for the circuit to work, A and E have to work. Consequently, this problem can be broken down into two pieces -- relays A and E, and the portion of the circuit between A and E -- because of the assumption of independence.
   Ignoring A and E for the moment, current will flow if B works, or C and D work, or B and C and D work. This is just the union formula given in (19) of notes #1. In this context it is:
   P(B È [C Ç D]) = P(B) + P(C Ç D) - P(B Ç C Ç D) =
   .8 + .64 - .8 * .64 = .928
   So our answer is: .8 * .928 * .8 = .594
   
   
4. Definition: Conditional Probability
   P(A|B) = P(A Ç B)/P(B)
   
   
5. Example: We roll two dice. I tell you that the sum of the two faces is equal to 8. What is the probability that one of the faces is a 3?
   Note that what conditional probability is a redefinition of the Sample Space. When we say "The probability of A given B", the set B is now our sample space. That is, this
   

   

   becomes this:
   

   

   In this problem, our sample space is now: B = {6,2 5,3 4,4 3,5 2,6}
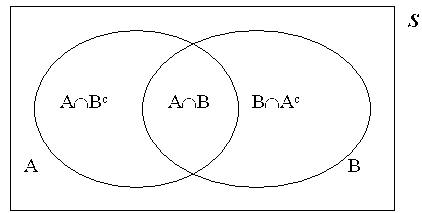
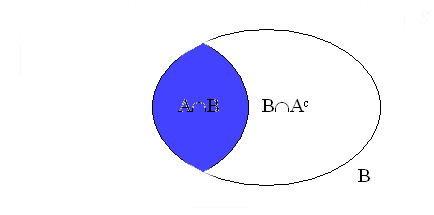
   The event A, is simply the set: A = {5,3 3,5}
   Hence: P(A Ç B) = 2/36 and P(B) = 5/36; so that:
   P(A|B) = P(A Ç B)/P(B) = (2/36)/(5/36) = 2/5
   
   
6. All probabilities are conditional probabilities. With respect to the orginal sample space, S, the probability of the event A can be written as:
   P(A|S) = P(A Ç S)/P(S)
   But this seems redundant because, by the the 2nd axiom of probability, P(S) = 1; and
   and P(A|S) = P(A). However, writing P(A) is just a shorthand for this.
   
   
7. Example: We draw a card randomly from a deck of 52 playing cards. If the card is a club, what is the probability that it is a King?
   Answer: P(King|Club) = P(King Ç Club)/P(Club) = P(King and Club)/P(Club) = (1/52)/(13/52) = 1/13
   
   
8. Example: We toss two coins. If at least one coin is a head, what is the probability that both coins are heads?
   Answer: P(HH|{HT, TH, HH}) = P(HH and {HT, TH, HH})/P({HT, TH, HH}) =
   P(HH)/P({HT, TH, HH}) =(1/4)/(3/4) = 1/3
   
   
9. Example (a very old problem): The King comes from a family of two children. What is the probability that the other child is his sister?
   Answer: Let B be the event "boy" and G be the event "girl". The sample space is:
   S = {BB, BG, GB, GG}. We are asked to compute the conditional probability:
   P(G|B) = P(G Ç B)/P(B) = P({BG, GB})/P({BB, BG, GB}) =(2/4)/(3/4) = 2/3
   
   
10. Problem 2.50 p.49 MWS. Let U be the event "Unsatisfied With Plumbing Job" and let A be the event "Plumber A does the job". We are given
    P(U) = .1 and P(A) = .4
    We are also told that half the complaints dealt with plumber A. Hence
    P(U|A) = .5
    
    
    1. We are asked to solve for P(U|A). This is
       P(U|A)=P(U Ç A)/P(A) = {P(U)P(A|U)}/P(A) = {.1 x .5}/.4 = .125
       
       
    2. We are asked to solve for P(U^c|A). This is
       P(U^c|A) = 1 - P(U|A) = 1 - .125 = .875
       
       
11. Alan and Betty are students in Prob-Stat. Alan attends class 70% of the time and Betty attends class 60% of the time and their absences are independent. If at least one of them is in class on a given day, what is the probability that both are in class on that day?
    We are given that P(A) = .7 and P(B) = .6. Also we know that at least one in this context means A È B. Hence:
    P(A|A È B) = P(A Ç [A È B]) /P(A È B) = P(A)/P(A È B)
    Now: P(A È B) = P(A) + P(B) - P(A Ç B) So that all we need to solve this problem is P(A Ç B). However, we are told that attendance is independent, so we can use (2) above and write:
    P(A)/P(A È B) = P(A)/[P(A) + P(B) - P(A)P(B)] =
    .7/(.7 + .6 - .42) = .7/.88 = .795
    
    In the language of Bayesian Statistics .795 is a Posterior probability and .7 is a Prior probability. The information -- "at least one is in class" -- causes us to revise or update our prior probability. Namely, the information rules out the outcome that both Alan and Betty are in class. Hence, in this case, the posterior probability must be higher than the prior probability!