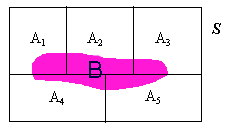
B = (A1 Ç B) È (A2 Ç B) È (A3 Ç B) È etc.
Now, using the identity: P(B|Ai) = P(B Ç Ai)/P(Ai), and rearranging:
P(Ai Ç B) = P(Ai)P(B|Ai). So that:
P(B) = P(A1)P(B|A1) + P(A2)P(B|A2) + P(A3)P(B|A3) + etc.
This allows us to state the famous Bayes Theorem.
Let A1, A2, ... , Ak be a partition of S such that P(Ai) > 0 for all i,
and let B be an event such that P(B) > 0. Then:
P(Ai|B) = [P(Ai)P(B|Ai)]/ [åj=1,k P(Aj)P(B|Aj)] =
P(Ai Ç B)/ [åj=1,k P(Aj Ç B)] =
P(Ai Ç B)/P(B)
Example: We have three chests, each with two drawers. (The chests are identical in every respect.) In one chest there is a silver coin in one drawer and a silver coin in the second drawer. In a second chest there is a gold coin in one drawer and a silver coin in the second drawer. And in the third chest there is a gold coin in each drawer.
We randomly select a chest and open a drawer. What is the probability that the un-opened drawer contains a gold coin?
Let A1, A2, A3, represent the three chests, and let B be the event "gold coin in the drawer". Clearly:
P(A1) = P(A2) = P(A3) = 1/3; and:
P(B|A1) = 0, P(B|A2) = 1/2, P(B|A3) = 1.
Only if we chose the 3rd chest could there be a second gold coin. Hence, we need to compute:
P(A3|B) = [P(A3)P(B|A3)]/ [åj=1,3 P(Aj)P(B|Aj)] =
= (1/3 x 1)/(1/3 x [0 + 1/2 + 1]) = 2/3.
Voting Example: In a particular city we have three kinds of voters: Republicans, Democrats, and Reformers, which we represent as the events R, D, and J, respectively. Let V be the event "voted in the last election". We are given that:
P(R) = .4, P(D) = .35, and P(J) = .25; and:
P(V|R) = .7, P(V|D) = .65, P(V|J) = .4.
We randomly select a person and learn that she did not vote. What is the probability that she is a Democrat?
By the rule of the complement:
P(Vc|R) = .3, P(Vc|D) = .35, P(Vc|J) = .6.
The probability we need to compute is:
P(D|Vc) = [P(D)P(Vc|D)]/
[P(D)P(Vc|D) + P(R)P(Vc|R)] + P(J)P(Vc|J)]
= (.35 x .35)/[(.35 x .35) + (.4 x .3) + (.25 x .6)] = .312
Problem 2.83 p.63
Let D be the event "Disease" and B be the event "Positive Test". We are given in the problem statement that:
P(D) = .01 so that P(Dc) = .99;
P(B|D) = .9 and P(Bc|Dc) = .9.
We are asked to compute:
P(D|B) = [P(D)P(B|D)]/[P(D)P(B|D) + P(Dc)P(B|Dc)] =
= (.01 * .9)/[(.01 * .9) + (.99 * .1)] = .0833.
Note that P(D|B) > P(D). That is, we start with a prior probability of .01 that any randomly chosen person has the disease. Then we are given information ("postive test"). This must raise the probability that the person has the disease. This probability is our posterior probability. In the jargon of Bayesian statistics, we have revised our priors in light of the information.
Also note that the probability 1 - P(D|B) is the probability of a false positive. This is not a costly error in this context. Far more costly is a false negative which in the context of disease testing means that you tell a sick person that they are not sick and send them back into the population to spread the disease. This probability is:
P(D|Bc) = [P(D)P(Bc|D)]/ [P(D)P(Bc|D) + P(Dc)P(Bc|Dc)] =
= (.01 * .1)/[(.01 * .1) + (.99 * .9)] = .00112.
Given how costly this error is the goal of disease testing is to drive this probability to zero while keeping P(D|B) as high as possible.
Problem 2.93 p.64
We have five bowls, i=1, 2, 3, 4, 5, with i white and 5-i black balls in the ith bowl, respectively. The experiment consists of randomly choosing a bowl and randomly drawing two balls from the bowl without replacement. That is, we simply take two balls out of the bowl (in contrast, drawing with replacement means that we would take one ball out, note its color, drop it back into the bowl, and then take another ball out and note its color).
Part (a): What is the probability that both balls are White?
Let A1, A2, ..., A5, represent the five bowls, and let B be the event "two White balls are drawn". Namely:
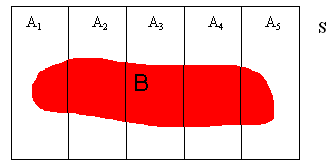
P(A1) = P(A2) = ... = P(A5) = 1/5; and:
P(B|A1) = 0
P(B|A2) = {[2 choose 2][3 choose 0]}/[5 choose 2] = 1/10
P(B|A3) = {[3 choose 2][2 choose 0]}/10 = 3/10
P(B|A4) = {[4 choose 2][1 choose 0]}/10 = 6/10
P(B|A5) = [5 choose 2]/10 = 1
Hence:
P(B) =[åj=1,5 P(Aj)P(B|Aj)] = (1/5)( 0 + 1/10 + 3/10 + 6/10 +1) = 2/5
Part (b): Given that both balls are White, what is the probability that they were drawn from bowl 3?
This is the probability:
P(A3|B) = P(A3 Ç B)/P(B) = [P(A3)P(B|A3)]/P(B)] =
(1/5 x 3/10)/(2/5) = 3/20