LEGACY CONTENT. If you are looking for Voteview.com, PLEASE CLICK HERE

This site is an archived version of Voteview.com archived from University of Georgia on May 23, 2017. This point-in-time capture includes all files publicly linked on Voteview.com at that time. We provide access to this content as a service to ensure that past users of Voteview.com have access to historical files. This content will remain online until at least January 1st, 2018. UCLA provides no warranty or guarantee of access to these files.

45-733 PROBABILITY AND STATISTICS I Notes #2A


January 2000


Discrete Random Variables

  1. Definition: Random Variable
    A variable the value of which is a number determined by the outcome of an experiment.
  2. Example: We flip a coin. Let X = 1 if Heads, and let X = 0 if Tails.
  3. Example: We roll a die. Let X = "number of dots".
  4. Definition: Probability Distribution: A function that assigns probabilities to the values of a random variable.
  5. Example: We flip a coin. Given the definition of a random variable in (2), let the probability distribution be:
    

                              æ1/2 x = 0   
                              ç
                       f(x) = ç1/2 x = 1
                              ç
                              è 0 otherwise
    6. A plot of this function looks like this: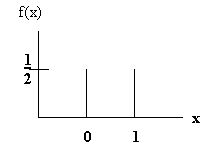

  6. Note that it is essential that the function, f(x), be defined for all possible values of the argument, x -- in this case, the entire real line. Consequently, the "0 otherwise" is not trivial!
  7. Example: We roll two dice. Let X = "sum of the two faces" and let the probability distribution be:
    
                              æ1/36  x = 2 or x = 12
                              ç
                              ç2/36  x = 3 or x = 11
                              ç
                              ç3/36  x = 4 or x = 10
                              ç
                       f(x) = ç4/36  x = 5 or x = 9
                              ç
                              ç5/36  x = 6 or x = 8
                              ç
                              ç6/36  x = 7   
                              ç
                              è 0 otherwise
  8. Properties of Discrete Probability Distributions
    a) f(xi) ³ 0 for all i
    b) åi=1,n f(xi) = 1
    c) P[a £ X £ b] = å f(xi)
  9. Example: With respect to (8):
    P[6 £ X £ 9] = P[X = 6] + P[X = 7] + P[X = 8] + P[X = 9] =
    1/36(5 + 6 + 5 + 4) = 20/36 = 5/9

    Note that: P[6 < X £ 9] = P[7 £ X £ 9]

  10. Definition: Distribution Function
    F(x) = P(X £ x)
  11. Example: With respect to (8):
    F(5) = P[X = 1] + P[X = 2] + P[X = 3] + P[X = 4] + P[X = 5] =
    1/36(1 + 2 + 3 + 4) = 10/36 = 5/18
  12. Note that, when working with discrete distributions that:
    P[X < 5] = F(4)
    P[5 £ X £ 8] = F(8) - F(4)
    P[5 £ X < 8] = F(7) - F(4)
    P[5 < X < 8] = F(7) - F(5)
  13. Discrete Uniform Distribution
    
                         æ1/n x = 1,2,3,4,5,...,n
                  f(x) = ç
                         è 0 otherwise
    A graph of the function looks like this: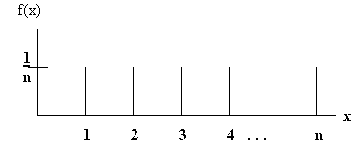

  14. Examples of the Discrete Uniform Distribution
    P[X £ 3] = 3/n
    P[4 £ X £ n] = 1 - P[X < 4] = 1 - F(3) = (n-3)/n
    F(5) = 5/n
  15. Bernoulli Distribution
    A Bernoulli experiment or trial is an experiment with only two possible outcomes. Traditionally these are known as a success and a failure. Let X = 1 be a success, and X = 0 be a failure, and let p be the probability: P(X = 1). Hence:
    
                         æ p  x = 1
                         ç
                  f(x) = ç1-p x = 0
                         ç
                         è 0 otherwise
  16. Binomial Distribution
    Let X1, X2, X3, ..., Xn be random variables corresponding to n Bernoulli trials (experiments), and let Z be the random variable:
    Z = åi=1,n Xi
    The distribution of Z is the binomial
    
                         æ ænö
                         ç ç ÷ pz(1-p)(n-z)
                  f(z) = ç èzø          z=0,1,2,3,...,n
                         ç
                         è 0 otherwise
  17. Example: Let n = 4 and p = 1/2, then
    P[Z = 2] = (4 choose 2)(1/2)2(1/2)2 = 6/16 = 3/8
  18. Problem 3.1 p.79. Let A and B be the two impurities. We are given that P(A) = .4, P(B)= .5, and
    1 - P(A È B) = .2. Hence
    P(A È B) = .8 and
    P(A È B) = P(A) + P(B) - P(A Ç B) = .4 + .5 - P(A Ç B) = .8. Hence
    P(A Ç B) = .1
    Let Y = number of impurites. Clearly P(Y = 2) = P(A Ç B) = .1
    and P(Y = 0) = 1 - P(A È B) = .2. Hence
    
                         æ .2  y = 0
                         ç
                         ç .7  y = 1
                  f(y) = ç
                         ç .1  y = 2
                         ç
                         è  0 otherwise
    To see that P(Y = 1) = .7, note that the shaded areas below correspond to this probability.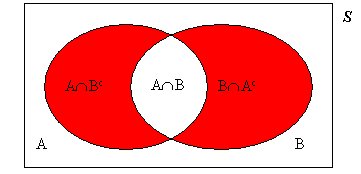

    Hence, P(Y = 1) = P(A È B) - P(A Ç B) = .8 - .1 = .7
  19. Problem 3.3 p.79
    Let D = "Defective". Let Y be a random variable and let it equal the number of the test on which the 2nd defective is found. Clearly
    P(Y = 2) = P(D on draw 1)* P(D on draw 2) = 1/2 * 1/3 = 1/6
    P(Y = 3) = P(D on draw 1) * P(Dc on draw 2) * P(D on draw 3) + P(Dc on draw 2) * P(D on draw 1) * P(D on draw 3)
    Hence: P(Y = 2) = 1/2*2/3*1/2 + 1/2*2/3*1/2 = 2/6
    Using similar reasoning:
    P(Y = 4) = 1/2*2/3*1/2*1 + 1/2*2/3*1/2*1 + 1/2*1/3*1*1 = 3/6 
    
                         æ  1/6  y = 2
                         ç
                         ç  2/6  y = 3
                  f(y) = ç
                         ç  3/6  y = 4
                         ç
                         è   0 otherwise