LEGACY CONTENT. If you are looking for Voteview.com, PLEASE CLICK HERE

This site is an archived version of Voteview.com archived from University of Georgia on May 23, 2017. This point-in-time capture includes all files publicly linked on Voteview.com at that time. We provide access to this content as a service to ensure that past users of Voteview.com have access to historical files. This content will remain online until at least January 1st, 2018. UCLA provides no warranty or guarantee of access to these files.

45-733 PROBABILITY AND STATISTICS I Notes #2B


January 2000


Continuous Random Variables

  1. Continuous Distributions
    P[X Î A] = òA f(x)dx
  2. Properties of Continuous Probability Distributions
    a) f(x) ³ 0 over the real line
    b) òf(x)dx = 1 over the real line
    c) P[a £ X £ b] = òab f(x)dx = F(b) - F(a)
  3. P(X = x) = 0. To see this:
    P(X = a) = òaa f(x)dx = F(a) - F(a) = 0
  4. Continuous Uniform Distribution
    
                         æ c  a < x < b
                  f(x) = ç
                         è 0 otherwise
    This is what the function looks like: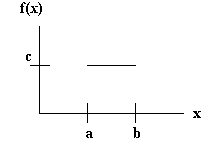

  5. To solve for the constant, c, use (b) in (22). That is:
    òab cdx = cx|ab = c[b-a] = 1; hence, c = 1/(b-a)
  6. Example: Let f(x) be:
    
                         æ c(1 - x3)  0 < x < 1
                  f(x) = ç
                         è   0 otherwise
    Find c.
    ò01 c(1 - x3)dx = c[x - x4/4]|01 = c[1 - 1/4] = c(3/4) = 1
    Hence, c = 4/3

    Find F(1/2).
    F(1/2) = P(X < 1/2) = ò01/2 (4/3)(1 - x3)dx = (4/3)[x - x4/4]|01/2 =
    (4/3)[1/2 - 1/64] = 31/48
  7. Example: Let f(x) be:
    
                         æ c/x  0 < x < 1
                  f(x) = ç
                         è 0 otherwise
    Find c.
    ò01 cxdx = clnx|01 = c[0 - - ¥] = ??
    So this is not a probability distribution.

  8. Problem 4.8 p.145
    
                         æ c(2 - y)  0 < y < 2
                  f(y) = ç
                         è 0 otherwise
    1. Find c
      ò02 c(2 - y)dy = c[2y - y2/2]|02 = c(4 - 4/2) = 2c
      Hence, c = 1/2

    2. Find F(y)
      F(y) = P(Y < y) = ò0y 1/2(2 - t)dt =
      1/2[2t - t2/2]|0y = 1/2(2y - y2/2) = y - y2/4      . Hence:
      
                         æ   0   y < 0
                         ç
                  F(y) = ç  y - y2/4  0 £ y £ 2
                         ç 
                         è   1   y > 2