LS GNP C MILMOB
============================================================
LS // Dependent Variable is GNP
Date: 04/04/98 Time: 21:54
Sample: 1915 1988
Included observations: 74
============================================================
Variable CoefficienStd. Errort-Statistic Prob.
============================================================
C 3.025348 0.547696 5.523772 0.0000
MILMOB 3.697863 0.547363 6.755782 0.0000
============================================================
R-squared 0.387966 Mean dependent var 3.061841
Adjusted R-squared 0.379466 S.D. dependent var 5.980692
S.E. of regression 4.711230 Akaike info criter 3.126553
Sum squared resid 1598.089 Schwarz criterion 3.188825
Log likelihood -218.6839 F-statistic 45.64060
Durbin-Watson stat 1.266900 Prob(F-statistic) 0.000000
============================================================
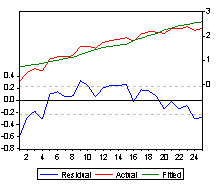
To test whether or not the period 1915-1945 has the same linear
specification as the period 1946-1988, we perform the Chow
Breakpoint Test.CHOW 1946
============================================================ Chow Breakpoint Test: 1946 ============================================================ F-statistic 0.079328 Probability 0.923820 Log likelihood ratio 0.167533 Probability 0.919646 ============================================================So we do not reject the null hypothesis.
WINDMILL.WF1 Examples.
============================================================
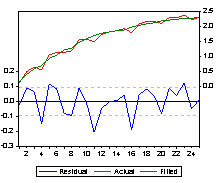
LS // Dependent Variable is DCOUT
Date: 04/04/98 Time: 22:01
Sample: 1 25
Included observations: 25
============================================================
Variable CoefficienStd. Errort-Statistic Prob.
============================================================
C 0.130875 0.125989 1.038779 0.3097
WIND 0.241149 0.019049 12.65927 0.0000
============================================================
R-squared 0.874493 Mean dependent var 1.609600
Adjusted R-squared 0.869036 S.D. dependent var 0.652278
S.E. of regression 0.236052 Akaike info criter-2.810787
Sum squared resid 1.281573 Schwarz criterion -2.713277
Log likelihood 1.661381 F-statistic 160.2571
Durbin-Watson stat 0.536610 Prob(F-statistic) 0.000000
============================================================