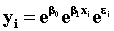
LEGACY CONTENT. If you are looking for Voteview.com, PLEASE CLICK HERE

This site is an archived version of Voteview.com archived from University of Georgia on May 23, 2017. This point-in-time capture includes all files publicly linked on Voteview.com at that time. We provide access to this content as a service to ensure that past users of Voteview.com have access to historical files. This content will remain online until at least January 1st, 2018. UCLA provides no warranty or guarantee of access to these files.

Probability and Statistics Name_________________________________

Spring 1998 45-734

Midterm Exam

Keith Poole

 

(20 Points)

1. Consider the following EVIEWS output from the second homework problem. Use it to answer parts (a) through (d) below.

============================================================
LS // Dependent Variable is TENSILE                                   
Date: 03/28/98   Time: 17:04                                          
Sample: 1 19                                                          
Included observations: 19                                             
============================================================
      Variable      CoefficienStd. Errort-Statistic  Prob.            
============================================================
         C           21.32126   5.430178   3.926439   0.0011          
      HARDWOOD       1.770986   0.647814   2.733788   0.0141          
============================================================
R-squared            0.305374    Mean dependent var 34.18421          
Adjusted R-squared   0.264513    S.D. dependent var 13.77777          
S.E. of regression   11.81589    Akaike info criter 5.038191          
Sum squared resid    2373.458    Schwarz criterion  5.137605          
Log likelihood      -72.82264    F-statistic        7.473597          
Durbin-Watson stat   0.246890    Prob(F-statistic)  0.014140          
============================================================
  1. (5 Points) Test the null hypothesis that b 0 = 0 against the alternative b 0 ¹ 0 using

    2. a = .00001.

     

    Do not reject the null hypothesis: P-Value > .00001.

     

     

     

  2. 5 Points) Test the null hypothesis that b 1 = 2.0 against the alternative b 1 ¹ 2.0 using

    3. a = .05.

    t.025,17 = 2.11

    Test Statistic = (1.770986 – 2)/.647814 = -.3535

    Since –2.11 < -.3535 < 2.11, We do not reject the null hypothesis.

     

     

    Probability and Statistics Name_________________________________

    Spring 1998 45-734

    Midterm Exam

    Keith Poole

  3. (5 Points) Construct 99% confidence limits for b 1.

    4. t.005,17 = 2.898

    1.770986 ± 2.898*.647814, or (-.106379 , 3.648351)

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

  4. (5 Points) Give a one sentence interpretation of the coefficient of HARDWOOD.

A one unit increase in HARDWOOD produces a 1.770986 unit increase in TENSILE.

 

 

 

 

 

 

 

 

Probability and Statistics Name_________________________________

Spring 1998 45-734

Midterm Exam

Keith Poole

(10 Points)

2. What numbers belong in the spaces marked (a) and (b) in the following EVIEWS output.

a) (5 Points)

 

t.1,17 = 1.333

 

 

 

 

 

 

b) (5 Points)

 

 

Std. Error = Coefficient/T-Stat = -0.668089/-2.661159 = .2510519

 

 

 

 

============================================================
LS // Dependent Variable is Y                               
Date: 03/28/98   Time: 17:41                                
Sample: 1 20                                                
Included observations: 20                                   
============================================================
     Variable     Coefficient Std. ErrorT-Statistic  Prob.  
============================================================
        C            2.280695   0.475395   4.797476   0.0002
        X1           0.349817                 (a)     0.2000
        X2          -0.668089      (b)    -2.661159   0.0165
============================================================
R-squared            0.298305    Mean dependent var 2.119493
Adjusted R-squared   0.215753    S.D. dependent var 2.377157
S.E. of regression   2.105156    Akaike info criter 1.626260
Sum squared resid    75.33860    Schwartz criterion 1.775620
Log likelihood      -41.64137    F-statistic        3.613528
Durbin-Watson stat   1.332075    Prob(F-statistic)  0.049233
============================================================

Probability and Statistics Name_________________________________

Spring 1998 45-734

Midterm Exam

Keith Poole

(10 Points)

3. With reference to the EVIEWS output used in question 2:

a) (5 Points) State the null hypothesis that is tested by the F-statistic. Is this hypothesis rejected at the 5% significance level?

H0: b 1 = b 2 = 0

 

Yes, the null hypothesis is rejected, P-Value < .05.

 

 

 

 

 

b) (5 Points) What is SSY for this regression?

SSY = (2.377157)2*19 = 107.36663

Probability and Statistics Name_________________________________

Spring 1998 45-734

Midterm Exam

Keith Poole

(10 Points)

  1. Use the HARDWOOD.WF1 data set from the 2nd Homework problem to perform the following tests:

    2. a) (5 Points) Perform the Chow Breakpoint test at the 9th observation and report the p-value. Do you reject or not reject the null hypothesis and what does that mean substantively?

     

    P-Value = .00062. The Null hypothesis here is that observations 1 – 8 have the same linear structure as observations 9 – 19. We reject the null hypothesis. Substantively, it appears as though different models fit these two sets of observations.

    b) (10 Points) Perform the Ramsey Reset Test. Try 3, then 2, then 1 fitted terms and report the three p-values. What is your interpretation of these three p-values and what do they tell you about the relationship between TENSILE and HARDWOOD?

    The P-Values are all 0.000000. This indicates that the simple linear specification is not correct. A good strategy to follow would be to try adding powers of HARDWOOD to the specification. In particular, the Rest Test at 2 shows that Y-Hat is significant squared and cubed. Reset Test at 3 shows all Y-Hat powers to be individually insignificant. Hence, trying:

    LS TENSILE C HARDWOOD HARDWOOD^2 would be a good start.

     

     

     

    Probability and Statistics Name_________________________________

    Spring 1998 45-734

    Midterm Exam

    Keith Poole

    (10 Points)

  2. On this page and the next page you will find EVIEWS output for a regression with 4 independent variables. The first output shows the model run for all 27 observations while the second and third outputs are for the first 13 observations and the final 14 observations respectively. Test the null hypothesis that observations 1 - 13 and observations 14 - 27 have the same linear model (Use a = .05).

    3.  

    SSEUR = 47.78610 + 64.04799 = 111.83409

    SSER = 202.6925

    F5,17,.05 = 2.81

    Test Statistic = [(202.6925 – 111.83409)/5]/[111.83409/17] = 2.76

    Since 2.76 < 2.81, Do not reject the null hypothesis.

     
    ============================================================
LS // Dependent Variable is Y                               
Date: 03/28/98   Time: 19:24                                
Sample: 1 27                                                
Included observations: 27                                   
============================================================
     Variable     Coefficient Std. ErrorT-Statistic  Prob.  
============================================================
        C            2.911143   1.644876   1.769825   0.0906
        X1          -0.114837   0.651213  -0.176344   0.8616
        X2           0.908389   0.352389   2.577802   0.0172
        X3          -1.919070   1.822874  -1.052772   0.3039
        X4          -2.551981   0.750349  -3.401058   0.0026
============================================================
R-squared            0.550582    Mean dependent var 1.309189
Adjusted R-squared   0.468869    S.D. dependent var 4.164922
S.E. of regression   3.035341    Akaike info criter 2.386224
Sum squared resid    202.6925    Schwartz criterion 2.626193
Log likelihood      -65.52536    F-statistic        6.738045
Durbin-Watson stat   2.162684    Prob(F-statistic)  0.001066
============================================================
============================================================
LS // Dependent Variable is Y                               
Date: 03/28/98   Time: 19:25                                
Sample: 1 13                                                
Included observations: 13                                   
============================================================
     Variable     Coefficient Std. ErrorT-Statistic  Prob.  
============================================================
        C           -0.028963   2.405406  -0.012041   0.9907
        X1           4.337600   2.063752   2.101803   0.0687
        X2           1.915258   0.606572   3.157513   0.0134
        X3          -4.357744   3.039306  -1.433796   0.1895
        X4           3.035299   2.598807   1.167958   0.2765
============================================================
R-squared            0.636701    Mean dependent var 1.430997
Adjusted R-squared   0.455051    S.D. dependent var 3.310762
S.E. of regression   2.444026    Akaike info criter 2.071016
Sum squared resid    47.78610    Schwartz criterion 2.288304
Log likelihood      -26.90781    F-statistic        3.505105
Durbin-Watson stat   2.262544    Prob(F-statistic)  0.061787
============================================================

============================================================
LS // Dependent Variable is Y                               
Date: 03/28/98   Time: 19:25                                
Sample: 14 27                                               
Included observations: 14                                   
============================================================
     Variable     Coefficient Std. ErrorT-Statistic  Prob.  
============================================================
        C            3.659305   2.427713   1.507305   0.1660
        X1          -1.951862   0.859362  -2.271291   0.0493
        X2           1.364739   0.519494   2.627053   0.0275
        X3          -3.970569   2.592990  -1.531271   0.1601
        X4          -3.521417   0.808209  -4.357062   0.0018
============================================================
R-squared            0.799289    Mean dependent var 1.196081
Adjusted R-squared   0.710084    S.D. dependent var 4.954448
S.E. of regression   2.667666    Akaike info criter 2.234861
Sum squared resid    64.04799    Schwartz criterion 2.463096
Log likelihood      -30.50917    F-statistic        8.960135
Durbin-Watson stat   1.758126    Prob(F-statistic)  0.003342
============================================================

     

    Probability and Statistics Name_________________________________

    Spring 1998 45-734

    Midterm Exam

    Keith Poole

    (10 Points)

  3. Use GSIA.WF1 to reproduce the output shown on page V-21 of the Epple Notes. Use the Wald Test option to test the joint hypothesis that the coefficient of ESSAY is equal to the coefficient of LETRAT and the coefficient of VGMAT to equal the coefficient of QGMAT. Report the p-value of the test and what is your substantive conclusion?

P-Value = .582785, thus we do not reject the null hypothesis that the two pairs of coefficients are equal. In other words, there is not a significant difference between a one point increase in the essay score and a one point increase in the letter rating score; and there is not a significant difference between a one point increase in verbal GMAT and a one point increase in quantitative GMAT.

 

 

Probability and Statistics Name_________________________________

Spring 1998 45-734

Midterm Exam

Keith Poole

(10 Points)

7. Consider the model:

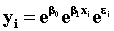
where:

E(e i )=0 for all i

E(e i2 ) = s 2 for all i

E(e i e j ) = 0 for all i and j

x fixed for all i

(a) (5 Points) Suppose a regression of y against x and a constant is run for the n observations from this model (i.e., LS Y C X). The estimated residuals (RESID) are then plotted against x (i.e., SCAT RESID X). Illustrate below the pattern of dots that you would expect to see in this scatter plot.

For Example:

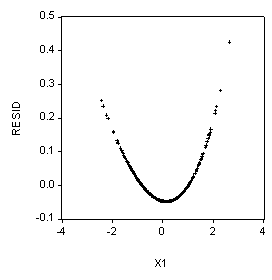
(b) (5 Points) Write below the EVIEWS commands that you would use to estimate this as a linear model.

LS LOG(Y) C X1

 

 

 

Probability and Statistics Name_________________________________

Spring 1998 45-734

Midterm Exam

Keith Poole

 

  1. Consider the regression reported below.

SSY = [(1.765115)2]*24 = 74.775143

SSE = [(0.832516)2]*20 = 13.861658

R2 = (74.775143 – 13.861658)/74.775143 = .8146

 
============================================================
LS // Dependent Variable is Y                               
Date: 03/28/98   Time: 16:16                                
Sample: 1 25                                                
Included observations: 25                                   
============================================================
     Variable     Coefficient Std. ErrorT-Statistic  Prob.  
============================================================
        C            0.585593   0.602372   0.972145   0.3426
        X1           1.419253   0.199449   7.115882   0.0000
        X2           2.658296   0.606784   4.380958   0.0003
        X3           0.712843   0.222854   3.198703   0.0045
        X4           0.563379   0.561315   1.003676   0.3275
============================================================
R-squared               ???      Mean dependent var 2.853512
Adjusted R-squared   0.777547    S.D. dependent var 1.765115
S.E. of regression   0.832516    Akaike info criter-0.189749
Sum squared resid       ???      Schwartz criterion 0.054026
Log likelihood      -28.10160    F-statistic        21.97194
Durbin-Watson stat   2.094706    Prob(F-statistic)  0.000000
============================================================

 

 

Probability and Statistics Name_________________________________

Spring 1998 45-734

Midterm Exam

Keith Poole

(10 Points)

  1. On the next page is a regression analysis of ice cream consumption (CONSUMP, in pints per capita) gathered at periodic intervals between March, 1951 and July, 1953. The theory being tested is that ice cream consumption should be a function of weekly family income (INCOME, in dollars), price (PRICE, dollars per pint), and mean temperature (TEMP, in Fahrenheit).
    1. Are the signs on the coefficients correct? Why or why not?

      2. Yes, the signs are correct. Economic theory tells us that ice cream consumption should increase with income, decrease in price, and, common sense tells us that it should increase with temperature. However, the coefficient on price is not statistically significant.
    2. Given your answer in part (a), what analyses would you now perform? State the relevant EVIEWS commands that would implement your answer.

Although the signs are correct, the fact that the price variable is not statistically significant merits some further investigation. A sensible first step would be to check the residuals by looking at scatterplots: e.g., SCAT RESID INCOME, SCAT RESID PRICE, SCAT RESID TEMP to see if there is anything suspicious.

Another useful step would be to drop PRICE and run the regression without it. That is:

LS CONSUMP C INCOME TEMP

Another route would be to run the Ramsey Reset Test to check for non-linear effects.

 
============================================================
LS // Dependent Variable is CONSUMP                                   
Date: 03/30/98   Time: 16:23                                          
Sample: 1 30                                                          
Included observations: 30                                             
============================================================
      Variable      CoefficienStd. Errort-Statistic  Prob.            
============================================================
         C           0.197315   0.270216   0.730212   0.4718          
       INCOME        0.003308   0.001171   2.823722   0.0090          
       PRICE        -1.044414   0.834357  -1.251759   0.2218          
        TEMP         0.003458   0.000446   7.762213   0.0000          
============================================================
R-squared            0.718994    Mean dependent var 0.359433          
Adjusted R-squared   0.686570    S.D. dependent var 0.065791          
S.E. of regression   0.036833    Akaike info criter-6.479173          
Sum squared resid    0.035273    Schwarz criterion -6.292346          
Log likelihood       58.61944    F-statistic        22.17489          
Durbin-Watson stat   1.021170    Prob(F-statistic)  0.000000          
============================================================