and place them in the same folder on a WINDOZE machine. PERFSTRT_2006.DAT looks like this:
SEN108KH.ORD
NON-PARAMETRIC MULTIDIMENSIONAL UNFOLDING OF 108th SENATE
2 675 20 36 10 21 20 0.005 5
(36A1,25000I1)
(I5,1X,36A1,2I5,50F8.3)
The first line is the roll call data file, the second line is the title, the third
line, in order, is the number of dimensions, the number of roll calls, the
number of iterations (leave as is), the number of "characters" to read off
the front of each legislator's record (leave as is), the record number of a
Senator that you believe is on the "Left" (this just sets "liberal" on the left --
lower ranks or negative values on the first dimension if the scaling is in
two or more dimensions -- and
"conservative" on the right), and the record number of a Senator that you
believe is on "Up" or on positive side of the second dimension (in the U.S. context,
these are the Southern Democrats in an earlier era). The last line is the format for
the coordinate output file. Please study the examples on the
Optimal Classification Program page because
we will be using this program several more times!- At the command line type
PERFL_2006
The program should only take a few seconds to run and it produces three output files -- PERF21.DAT, PERF23.DAT, and PERF25.DAT. PERF21.DAT should look something like this:30 APRIL 2007 17.06.38.00. RANDOM NUMBER SEED 44600 SEN108KH.ORD NON-PARAMETRIC MULTIDIMENSIONAL UNFOLDING OF 108th SENATE 2 675 20 36 10 21 20 0.005 (36A1,25000I1) (I5,1X,36A1,2I5,50F8.3) ****************************************************************************** 1 ROLL CALLS 2 2810 53605 0.05242 0.94758 0.85508 0.00000 LEGISLATORS 2 2744 53605 0.05119 0.94881 0.85848 0.00000 2 ROLL CALLS 2 2668 53605 0.04979 0.95021 0.86240 0.99586 LEGISLATORS 2 2655 53605 0.04953 0.95047 0.86307 0.99862 3 ROLL CALLS 2 2645 53605 0.04934 0.95066 0.86359 0.99848 LEGISLATORS 2 2634 53605 0.04914 0.95086 0.86416 0.99525 4 ROLL CALLS 2 2624 53605 0.04895 0.95105 0.86467 0.99847 LEGISLATORS 2 2621 53605 0.04889 0.95111 0.86483 0.99946 5 ROLL CALLS 2 2616 53605 0.04880 0.95120 0.86509 0.99780 LEGISLATORS 2 2613 53605 0.04875 0.95125 0.86524 0.99993 6 ROLL CALLS 2 2609 53605 0.04867 0.95133 0.86545 0.99968 LEGISLATORS 2 2606 53605 0.04861 0.95139 0.86560 0.99995 7 ROLL CALLS 2 2603 53605 0.04856 0.95144 0.86576 0.99803 LEGISLATORS 2 2600 53605 0.04850 0.95150 0.86591 0.99997 8 ROLL CALLS 2 2599 53605 0.04848 0.95152 0.86596 0.99817 LEGISLATORS 2 2599 53605 0.04848 0.95152 0.86596 0.99999 9 ROLL CALLS 2 2596 53605 0.04843 0.95157 0.86612 0.99957 LEGISLATORS 2 2595 53605 0.04841 0.95159 0.86617 0.99965 10 ROLL CALLS 2 2593 53605 0.04837 0.95163 0.86627 0.99957 LEGISLATORS 2 2592 53605 0.04835 0.95165 0.86632 0.99992 11 ROLL CALLS 2 2590 53605 0.04832 0.95168 0.86643 0.99965 LEGISLATORS 2 2587 53605 0.04826 0.95174 0.86658 0.99999 12 ROLL CALLS 2 2584 53605 0.04820 0.95180 0.86674 0.99930 LEGISLATORS 2 2583 53605 0.04819 0.95181 0.86679 0.99999 13 ROLL CALLS 2 2583 53605 0.04819 0.95181 0.86679 0.99986 LEGISLATORS 2 2583 53605 0.04819 0.95181 0.86679 1.00000 14 ROLL CALLS 2 2583 53605 0.04819 0.95181 0.86679 0.99998 LEGISLATORS 2 2582 53605 0.04817 0.95183 0.86684 0.99999 15 ROLL CALLS 2 2581 53605 0.04815 0.95185 0.86689 0.99975 LEGISLATORS 2 2580 53605 0.04813 0.95187 0.86694 0.99999 16 ROLL CALLS 2 2580 53605 0.04813 0.95187 0.86694 0.99994 LEGISLATORS 2 2579 53605 0.04811 0.95189 0.86699 1.00000 17 ROLL CALLS 2 2579 53605 0.04811 0.95189 0.86699 0.99933 LEGISLATORS 2 2578 53605 0.04809 0.95191 0.86704 1.00000 18 ROLL CALLS 2 2578 53605 0.04809 0.95191 0.86704 0.99999 LEGISLATORS 2 2578 53605 0.04809 0.95191 0.86704 1.00000 19 ROLL CALLS 2 2578 53605 0.04809 0.95191 0.86704 0.99992 LEGISLATORS 2 2578 53605 0.04809 0.95191 0.86704 1.00000 20 ROLL CALLS 2 2578 53605 0.04809 0.95191 0.86704 0.99979 LEGISLATORS 2 2578 53605 0.04809 0.95191 0.86704 1.00000 MEAN VOLUME LEG. 0.0098 0.0495 MACHINE PREC. 2 2578 53605 0.04809 0.95191 0.86704 MACHINE PREC. 2 2578 53605 0.04809 0.95191 0.86704 17.06.38.00. ELAPSED TIME OF JOB 17.07.36.37.The seventh column reports the correct classification. For the 108th Senate the algorithm quickly converges to 0.95191 (95.2%).
Turn in a copy of this file.
- The file PERF25.DAT contains the output coordinates for the Senators and
the roll calls. The first few lines of
PERF25.DAT for the Senators should look very similar to this:
30 APRIL 2007 17.06.38.00. 1 1089991099 0USA 200 BUSH 0 90 1.000 0.501 0.344 0.064 2 1084970041 0ALABAMA 20001SESSIONS 17 549 0.969 0.018 0.291 -0.114 3 1089465941 0ALABAMA 20001SHELBY 27 547 0.951 0.002 0.257 0.020 4 1084030081 0ALASKA 20025MURKOWSKI 23 532 0.957 0.002 0.232 0.097 5 1081210981 0ALASKA 20001STEVENS 19 554 0.966 0.009 0.242 0.109 6 1081542961 0ARIZONA 20001KYL 16 550 0.971 0.002 0.305 -0.290 7 1081503961 0ARIZONA 20001MCCAIN 46 545 0.916 0.002 0.206 -0.822 8 1084030142 0ARKANSA 10001PRYOR 23 554 0.958 0.005 -0.215 0.567 9 1082930542 0ARKANSA 10001LINCOLN 17 553 0.969 0.003 -0.200 0.576 10 1081501171 0CALIFOR 10001BOXER 11 536 0.979 0.002 -0.314 -0.208 etc etc etcThe last two columns are the two-dimensional coordinates. The party code is just to the right of the state name: 100=Democrat, 200=Republican. The state codes are to the left of the column of zeroes at the beginning of the state names.
The first few lines of PERF25.DAT for the Roll Calls (just below the Senators) should look very similar to this:1 1 51 46 1 48 53 6 1 0.978 0.026 0.603 -0.797 2 2 45 52 0 48 53 1 6 1.000 0.017 0.992 -0.126 3 3 45 52 0 48 53 1 6 1.000 0.017 0.992 -0.126 4 4 52 45 0 47 54 6 1 1.000 -0.123 0.997 -0.074 5 5 46 51 0 48 53 1 6 1.000 0.017 0.992 -0.126 6 6 52 46 1 48 53 6 1 0.978 0.025 0.605 -0.796 7 7 46 52 0 47 54 1 6 1.000 -0.123 0.997 -0.074 8 8 62 33 13 73 28 1 6 0.606 0.246 0.989 -0.148 9 10 88 4 2 96 5 1 6 0.500 0.294 0.998 -0.058 10 11 51 45 0 49 52 6 1 1.000 0.050 0.899 0.437 etc etc etcThe last two columns are the Normal Vector coordinates two-dimensional and the column immediately to the left of the Normal Vector Coordinates is the position on the Normal Vector where the Cutting Plane intersects.
Make a two-dimensional plot of the Cutting Planes and the Senator coordinates using the R program below:
 plot_oc_output_X_and_Z.r -- R
Program to Plot OC Cutting Line and Legislator Outputs
plot_oc_output_X_and_Z.r -- R
Program to Plot OC Cutting Line and Legislator Outputs
Use Epsilon to create the two files from PERF25.DAT that the R program reads. When you run the program you should see:

The "P" is President Bush. Modify the program to display the names of a few prominent Senators. Turn in the graph.
- The file PERF23.DAT has some miscellaneous diagnostics for the
program including the eigenvalues of the double-centered agreement score matrix.
Here is the relevant portion of the file:
etc. etc. PERFORMANCE INDEX EIGENVALUE/VECTOR ROUTINE= 2 101 0 0 1 12.7734 78.2262 78.2262 15.0802 70.5133 70.5133 2 0.3268 2.0014 80.2276 0.5582 2.6101 73.1234 3 0.2346 1.4370 81.6646 0.3818 1.7855 74.9088 4 0.1530 0.9368 82.6014 0.2805 1.3118 76.2206 5 0.1347 0.8252 83.4266 0.2585 1.2087 77.4294 6 0.1025 0.6279 84.0545 0.2383 1.1144 78.5438 7 0.0811 0.4965 84.5510 0.2132 0.9969 79.5408 8 0.0762 0.4668 85.0178 0.1844 0.8621 80.4029 9 0.0720 0.4409 85.4587 0.1613 0.7544 81.1572 10 0.0685 0.4193 85.8780 0.1518 0.7099 81.8672 11 0.0616 0.3774 86.2554 0.1355 0.6333 82.5005 12 0.0542 0.3321 86.5875 0.1253 0.5857 83.0862 13 0.0523 0.3204 86.9079 0.1214 0.5675 83.6537 14 0.0511 0.3128 87.2207 0.1182 0.5529 84.2066 15 0.0483 0.2957 87.5163 0.1151 0.5382 84.7448 16 0.0415 0.2542 87.7706 0.1091 0.5101 85.2548 17 0.0391 0.2394 88.0100 0.1004 0.4694 85.7242 18 0.0364 0.2232 88.2332 0.0993 0.4644 86.1886 19 0.0346 0.2118 88.4450 0.0976 0.4564 86.6449 20 0.0330 0.2023 88.6473 0.0909 0.4252 87.0701 etc. etc.The second column with a first entry of 12.7734 are the eigenvalues. Make a graph of the eigenvalues like the one you did for Homework 3 Q.3.d. In particular, you can modify the code below to do this:nrow <- 10 plot(T[,1],T[,2], xlab="", ylab="", main="", type="n",xlim=c(1,10),ylim=c(0.0,1.0),axes=FALSE) # # Main title: which side of the plot (1=bottom, 2=left, 3=top, 4=right). mtext("Normalized Eigenvalues of Double-Centered\n Agreement Score Matrix for the 104th Senate",side=3,line=2.75,cex=1.2) # x-axis title mtext("Dimension",side=1,line=2.75,cex=1.2) # y-axis title mtext("Normalized Eigenvalue",side=2,line=2.5,cex=1.2) # # I am tricking R to do a nice looking x-axis by forcing # the labels # axis(1,1:10, labels=c(' 1',' 2',' 3',' 4',' 5',' 6',' 7',' 8',' 9','10'), font=2,col.axis='black',cex.axis=1.2) # font switch: 1 corresponds to plain text, # 2 to bold face, 3 to italic and 4 to bold italic # the at=NULL tells R to compute tick marks internally axis(2,at=NULL,col.axis='black',cex.axis=1.2,font=2) # box() points(T[,1],T[,2],pch=16,col="red") lines(T[1:nrow,1],T[1:nrow,2],lty=1,lwd=3,col="blue")
- Use Epsilon to change the number of
dimensions from 2 to 1 in PERFSTRT_2006.DAT and run
PERFL_2006 again (be sure to save the output files from
the two-dimensional run first!!!! -- they will be overwritten by the new ones!).
PERF21.DAT should look something like this:
30 APRIL 2007 17.21.09.51. RANDOM NUMBER SEED 42300 SEN108KH.ORD NON-PARAMETRIC MULTIDIMENSIONAL UNFOLDING OF TEXAS DATA 1 675 20 36 10 21 20 0.005 5 (36A1,25000I1) (I5,1X,36A1,2I5,50F8.3) ****************************************************************************** 1 ROLL CALLS 1 3302 53605 0.06160 0.93840 0.82971 2 LEGISLATORS 1 3224 53605 0.06014 0.93986 0.83373 0.99820 3 ROLL CALLS 1 3167 53605 0.05908 0.94092 0.83667 4 LEGISLATORS 1 3156 53605 0.05888 0.94112 0.83724 0.99972 5 ROLL CALLS 1 3134 53605 0.05846 0.94154 0.83837 6 LEGISLATORS 1 3124 53605 0.05828 0.94172 0.83889 0.99989 7 ROLL CALLS 1 3112 53605 0.05805 0.94195 0.83950 8 LEGISLATORS 1 3109 53605 0.05800 0.94200 0.83966 0.99994 9 ROLL CALLS 1 3103 53605 0.05789 0.94211 0.83997 10 LEGISLATORS 1 3102 53605 0.05787 0.94213 0.84002 0.99994 11 ROLL CALLS 1 3098 53605 0.05779 0.94221 0.84023 12 LEGISLATORS 1 3097 53605 0.05777 0.94223 0.84028 0.99998 13 ROLL CALLS 1 3097 53605 0.05777 0.94223 0.84028 14 LEGISLATORS 1 3096 53605 0.05776 0.94224 0.84033 0.99999 SHARPEN 2 3090 53605 SHARPEN 3 3087 53605 SHARPEN 4 3085 53605 SHARPEN 5 3085 53605 L-PERMUTATIONS 5 3085 53605 0.05755 0.94245 0.84090 17.21.09.51. ELAPSED TIME OF JOB 17.25.18.87.The correct classification is now 94.245% (0.94245).
Turn in a copy of this file.
- The PERF25.DAT file
contains a rank ordering for the Senators and
the roll calls. The
first part of the file shows the Senators in rank order and then in the order
that they appear in the roll call file with their ranking:
30 APRIL 2007 17.21.09.51. 1 1081491412 0NEW JER 10001LAUTENBERG 24 548 0.956 1.000 2 1084010412 0NEW JER 10001CORZINE 28 545 0.949 2.000 3 10829142 5 0RHODE I 10001REED 24 551 0.956 3.000 4 10810808 3 0MASSACH 10001KENNEDY ED 17 530 0.968 4.000 5 10814213 1 0CONNECT 10001DODD 25 547 0.954 5.500 6 1081440082 0HAWAII 10001AKAKA 30 525 0.943 5.500 7 1081303952 0MARYLAN 10001SARBANES 8 543 0.985 7.000 8 1081120448 0SOUTH C 10001HOLLINGS 69 517 0.867 8.000 9 10814307 6 0VERMONT 10001LEAHY 32 545 0.941 9.500 10 108 136656 0WEST VI 10001BYRD ROBER 53 539 0.902 9.500 etc. etc. etc. 97 1089991099 0USA 200 BUSH 1 90 0.989 97.000 98 1081542961 0ARIZONA 20001KYL 22 550 0.960 98.000 99 1084970041 0ALABAMA 20001SESSIONS 20 549 0.964 99.000 100 1082953765 0NEVADA 20001ENSIGN 38 543 0.930 100.000 101 1081490853 0OKLAHOM 20001NICKLES DO 16 552 0.971 101.000 ****************************************************************************** 1 1089991099 0USA 200 BUSH 1 90 0.989 97.000 2 1084970041 0ALABAMA 20001SESSIONS 20 549 0.964 99.000 3 1089465941 0ALABAMA 20001SHELBY 29 547 0.947 70.000 4 1084030081 0ALASKA 20025MURKOWSKI 30 532 0.944 70.000 5 1081210981 0ALASKA 20001STEVENS 21 554 0.962 67.500 6 1081542961 0ARIZONA 20001KYL 22 550 0.960 98.000 7 1081503961 0ARIZONA 20001MCCAIN 88 545 0.839 93.500 8 1084030142 0ARKANSA 10001PRYOR 34 554 0.939 43.000 9 1082930542 0ARKANSA 10001LINCOLN 24 553 0.957 44.000 10 1081501171 0CALIFOR 10001BOXER 23 536 0.957 14.000 etc. etc. etc. 98 1084930925 0WISCONS 10001FEINGOLD 54 556 0.903 18.000 99 1081570325 0WISCONS 10001KOHL 35 549 0.936 34.000 100 1084970668 0WYOMING 20001ENZI 23 553 0.958 90.000 101 1081563368 0WYOMING 20001THOMAS 17 549 0.969 89.000Note that below the legislators are the rank positions for the roll call cutting points.
Use R to plot the rank-ordering of the Senators (horizontal axis) against the first dimension from the two-dimensional run done above (vertical axis). In the graph display the Pearson correlation between the two in a fashion similar to the way I displayed the STRESS value for the Weisberg & Rusk candidate configuration in Homework 4 Q.1 (in R the command to compute a Pearson correlation is cor(x,y) where x and y are two vectors).
and place them in the same folder on a WINTEL machine. Read the Aldrich-McKelvey scaling program page to see how to run the program.
Here are the first three lines of OLS68A.DAT.
1681 0 10 1 1 1 1 1 63 4 4 5 7 1 2 2 3 7 1 1
1124 0 10 1 0 0 0 1 82 1 1 4 4 1 1 1 1 4 1 5
78 5 10 1 0 1 1 1 78 2 1 5 7 4 5 5 6 6 7 5
The variables, in order, are:
RESPONDENT ID = unique 4 digit number
PARTY ID = 0 to 6 -- 0 = Strong Democrat
1 = Weak Democrat
2 = Lean Democrat
3 = Independent
4 = Lean Republican
5 = Weak Republican
6 = Strong Republican
RAW INCOME = **do not use**
FAMILY INCOME = income quintile 1 - 5
SEX = 0 Man, 1 Woman
RACE = 0 White, 1 Black
SOUTH = 0 North, 1 South
EDUCATION = 1 High School or less, 2 Some College, 3 College
AGE = In Years
URBAN UNREST SCALE = Johnson, Humphrey, Nixon, Wallace, Self-Placement
VIETNAM SCALE = Johnson, Humphrey, Nixon, Wallace, Self-Placement
VOTED = 1 Voted, 5 Did Not Vote
Run the Aldrich-McKelvey scaling procedure using both the urban unrest and
vietnam files. In particular, for the urban unrest scale here are the commands:MCKALNEW
Control Card File Name? URBAN68.CTL
Data File Name? OLS68A.DAT
Output File Name? URBAN.PRN
Coordinate Output File Name? URBAN.DAT
The program reads URBAN68.CTL and OLS68A.DAT and writes the output files to disk. The coordinates for the political stimuli are in URBAN.PRN. In particular, here is the relevant portion of URBAN.PRN:
etc etc etc
******************************************************************************
PERFORMANCE INDEX= 0
EIGENVALUES
-1070.0801
-936.8338
-251.0831
0.0012
******************************************************************************
******************************************************************************
STIMULUS COORDINATES
LBJ HHH NIXON WALLA
-0.3978 -0.4262 0.0116 0.8124 These are the coordinates
STIMULUS COORDINATES RAW DATA
-0.4087 -0.4229 0.0232 0.8084
******************************************************************************
CORRECTED GOODNESS OF FIT AND RAW FIT
0.0919 0.5075
etc etc etc
- Graph the scaled stimuli
coordinates against each other using R -- that is,
use the Vietnam coordinates as the horizontal axis and the Urban Unrest coordinates
as the vertical axis. Use the names of the candidates and label the graph and
the axes appropriately. Why do you think the plot looks the way it does?
- Use Epsilon to merge the party ID variable
from OLS68A.DAT into the coordinate output file. For example, here are the
first few lines of the coordinate output file for the urban unrest scale:
LINE # CASE # R POS ALPHA BETA SCALED POS RSQ 1 1681 1.0 -2.6243 0.5249 -2.0994 0.9994 0.9997 2 1124 1.0 -0.8831 0.3532 -0.5298 0.6790 0.8240 3 78 4.0 -0.9588 0.2557 0.0639 0.8992 0.9483 4 553 4.0 -1.2302 0.2895 -0.0724 0.6460 0.8037The second column is the respondent ID number. Use the respondent ID number to match OLS68A.DAT with the output file and insert the party ID code into the output file. After you have inserted the party code you can delete all the columns except the party code, BETA (you will need that for graphing), and the Scaled Position. If you have done everything correctly the first few lines of your file should look like this:0 0.5249 -2.0994 0 0.3532 -0.5298 5 0.2557 0.0639 1 0.2895 -0.0724 1 0.2763 0.6907 1 1.3930 -0.3482 0 1.0597 -0.5298 0 0.2322 -0.3482 0 0.4371 -0.8742 5 0.3901 0.6827 0 0.0033 0.0050 0 0.2119 -0.5298 1 0.2624 0.2624 2 0.2938 -0.5142 1 0.2745 0.1373 etc. etc. etc.Write an Epsilon text macro that inserts the party variable into the coordinate file. In the macro, use a split screen and place the coordinate file in the top screen and OLS68A.DAT in the bottom screen. When you begin it should look like this:

The beginning of the text macro should look like this:(define-macro "hw6" "C-U20C-F C-U5C-BC-KC-YC-DC-AC-X
Open up another window and put the above macro fragment in it and you should be here:C-Y C-U3C-F C-U4C-BC-KC-YC-DC-AC-X C-Y")

Finish constructing the macro and turn in the listing.
- Read the above file into R and
make smoothed histograms of the scaled positions of the respondents
by party ID. For example, to make smoothed histograms of the Strong Democrats
and Strong Republicans use this R Program:
 Smoothed_Histogram_hw_6_2006.r --
R Program to Plot Strong Democrats and Strong Republicans on Urban Unrest Scale
Smoothed_Histogram_hw_6_2006.r --
R Program to Plot Strong Democrats and Strong Republicans on Urban Unrest Scale
Here is what Smoothed_Histogram_hw_6_2006.r looks like:# # # Smoothed_Histogram_hw_6_2006.r -- Plots Strong Democrats and Strong Republicans on # 1968 Urban Unrest Scale # # rm(list=ls(all=TRUE)) # # library(MASS) # T <- matrix(scan("C:/UCSD_Homework_6/urban_hw6.txt",0),ncol=3,byrow=TRUE) # # Gore and Bush Voters # strong.democrat <- T[T[,1]==0 & T[,2] > 0,3] Select Strong Democrats With Positive Betas strong.republican <- T[T[,1]==6 & T[,2] > 0,3] Select Strong Republicans With Positive Betas # DemShare <- length(strong.democrat)/(length(strong.democrat)+length(strong.republican)) These two commands just compute RepShare <- length(strong.republican)/(length(strong.democrat)+length(strong.republican)) the proportions for the two Parties # demdens <- density(strong.democrat) density computes kernel density estimates. (Also see bandwidth.) demdens$y <- demdens$y*DemShare This is a trick so that the two densities.... # repdens <- density(strong.republican) repdens$y <- repdens$y*RepShare ...will add to 1.0 # ymax1 <- max(demdens$y) ymax2 <- max(repdens$y) ymax <- 1.1*max(ymax1,ymax2) # plot(demdens,main="", xlab="", ylab="", xlim=c(-1.5,1.5),ylim=c(0,ymax),font=2) lines(demdens,lwd=3,col="red") lines(repdens,lwd=3,col="blue") # text( .50,0.800,"Red = Strong Democrats",col="red",font=2,cex=1.2) text( .50,0.725,"Blue = Strong Republicans",col="blue",font=2,cex=1.2) # Main title mtext("Strong Party Identifiers\nFrom 1968 Urban Unrest 7-Point Scale",side=3,line=1.50,cex=1.2,font=2) # x-axis title mtext("Urban Unrest Scale Value",side=1,line=2.75,cex=1.2) # y-axis title mtext("Density",side=2,line=2.5,cex=1.2) # arrows(-.398, 0.06,-.398,0.0,length=0.1,lwd=3,col="red") text(-.308,.08,"LBJ",font=2) arrows(-.426, 0.06,-.426,0.0,length=0.1,lwd=3,col="red") text(-.516,.08,"HHH",font=2) arrows( .012, 0.13, .012,0.0,length=0.1,lwd=3,col="blue") text( .000,.16,"Nixon",font=2) arrows( .812, 0.13, .812,0.0,length=0.1,lwd=3,col="green") text( .812,.18,"Wallace",font=2) # # LBJ HHH NIXON WALLA # -0.3978 -0.4262 0.0116 0.8124Here is the graph it produces:

Turn in this plot.
- Similar to the above, make a graph for all Democrats (0,1,2) and all Republicans (4,5,6). Adjust the labeling
accordingly and make certain that everything is neatly presented.
- Similar to the above, make a graph for all Democrats (0,1,2) and all Republicans (4,5,6) for the
Vietnam scale. Adjust the labeling
accordingly and make certain that everything is neatly presented.
- Similar to the above, make a graph for all Democrats (0,1,2), all Republicans (4,5,6), and
Independents (4) for the Vietnam scale. Adjust the labeling
accordingly and make certain that everything is neatly presented. To do this note that you will
have to add code to compute IndShare and adjust everything so that the three smoothed histograms
add up to 1.
idno respondent id number partyid strength of party id -- 0 to 6 income raw income category incomeq income quintile -- 1 to 5 race 0 = white, 1 = black sex 0 = man, 1 = woman south 0 = north, 1 = south education 1=HS, 2=SC, 3=College age age in years uulbj lbj position urban unrest uuhhh humphrey pos urban unrest uunixon nixon position urban unrest uuwallace wallace pos urban unrest uuself self placement urban unrest vnmlbj lbj pos vietnam vnmhhh hhh pos vietnam vnmnixon nixon pos vietnam vnmwallace wallace pos vietnam vnmself self placement vietnam voted 1=voted, 5=did not vote votedfor who voted for -- 1 = humphrey, 2= nixon, 3=wallace wallace wallace therm humphrey humphrey thermometer nixon nixon thermometer mccarthy mccarthy thermometer reagan reagan thermometer rockefeller rockefeller thermometer lbj lbj thermometer romney romney thermometer kennedy robert kennedy thermometer muskie muskie thermometer agnew agnew thermometer lemay "bombs away with Curtis LeMay" thermometerThe control card file for the metric unfolding procedure is shown below. The first line has the name of the data file. The first number in the second line is the number of stimuli, the next two numbers are the minimum and maximum number of dimensions to estimate, and the "10" is the number of iterations.
The third line contains some "antique" options we will never use. The only numbers that matter on this line are the "4" which indicates the number of identifying characters to read off each line of the data file (e.g., the respondent id number), and the "2" at the end. This is the number of missing data codes which appear in the sixth line.
The first number in the fourth line is a tolerance value -- leave it as is. The next three numbers are parameters to transform the input data into squared distances. In this case, let amx=-.02, bmx=2.0, and cmx=2.0. The following equation transforms the thermometers into squared distances:
d2 = (amx*t+bmx)cmx
where t = input data. This formula takes a linear transformation of the input data to the power cmx. With amx = -.02, bmx = 2.0, and cmx = 2.0, this is equivalent to subtracting the thermometer score from 100, dividing by 50, and then squaring. This converts t from a 0-100 scale to a 4-0 scale. If the data, t, are distances, set amx = 1.0, bmx = 0.0, and cmx = 2.0. If the data are correlations, set amx = -1.0, bmx = 1.0, and cmx=2.0 or 1.0 if the correlations are initially regarded as unsquared or squared distances respectively.
The next value, "1.5", is the maximum absolute expected coordinate value on any dimension. It is used for plotting purposes. If the squared distances are confined to a 4-0 scale, xmax=1.5 is usually sufficient. The last two numbers, "0.0" and "100.0", are the minimum and maximum expected values of the input data. These are used to catch coding errors in the input data. Anything out of range is treated as missing data.
The fifth line is the format of the data file and the sixth line contains the missing data codes.
Finally, the last 12 lines are labels for the stimuli.
OLS68B.DAT
12 2 2 10 0 0
1 1 0 4 2
.001 -0.02 2.0 2.0 1.5 0.0 100.0
(1X,4A1,60X,12F3.0)
98 99
WALLACE
HUMPHREY
NIXON
MCCARTHY
REAGAN
ROCKEFELLER
LBJ
ROMNEY
R.KENNEDY
MUSKIE
AGNEW
LEMAY
- Run MLSMU6. It will produce an output
file called FORT.22. The first 20 lines look like this:
WALLACE 1.2646 0.5154 217.4823 0.5541 1242.0000 HUMPHREY -0.5559 0.3738 114.7892 0.6968 1252.0000 NIXON 0.1480 -0.5415 123.2209 0.5319 1250.0000 MCCARTHY -0.6251 -0.4938 151.8926 0.3854 1204.0000 REAGAN 0.3080 -0.8895 131.8091 0.4380 1212.0000 ROCKEFELLER -0.5579 -0.5995 148.1413 0.3724 1229.0000 LBJ -0.5223 0.4905 147.0334 0.5573 1253.0000 ROMNEY -0.4736 -0.7866 111.3147 0.3434 1167.0000 R.KENNEDY -0.4245 0.2351 148.8571 0.5418 1242.0000 MUSKIE -0.6611 0.1660 126.0836 0.4862 1177.0000 AGNEW 0.2341 -0.8706 114.1418 0.4675 1180.0000 LEMAY 1.1901 0.4267 174.3242 0.4601 1188.0000 1681 -0.0285 0.2555 0.7918 0.6824 12.0000 1124 -0.1768 0.2692 1.4788 0.6992 12.0000 78 0.5707 -0.1514 3.5611 0.2141 12.0000 553 0.1376 0.1064 0.1597 0.7047 9.0000 7 0.2542 0.1235 1.2634 0.0116 12.0000 412 0.2781 0.0867 0.1024 0.6197 12.0000 631 0.5017 0.1088 1.1196 0.0742 12.0000 1316 0.2175 -0.5842 1.1568 0.8577 12.0000 etc etc etc etc etc etcThe first two columns after the names are the two dimensional coordinates. The first 12 lines are the coordinates for the political candidates and lines 13 onward are the coordinates for the respondents. Use R to plot the 12 candidates in two dimensions. This plot should be very similar to the one you did for Question 1 above.
- Use Epsilon to insert the voted
and voted for variables into FORT.22 (strip off the candidate
coordinates first). Turn in the Epsilon macro
you used to do the insertion and the first 20 lines of the file.
- Use R to make two-dimensional plots
of the Voters, Non-Voters, Humphrey Voters only, Nixon Voters only, and
Wallace Voters only. For example, your Humphrey Voter plot should look
something like this:
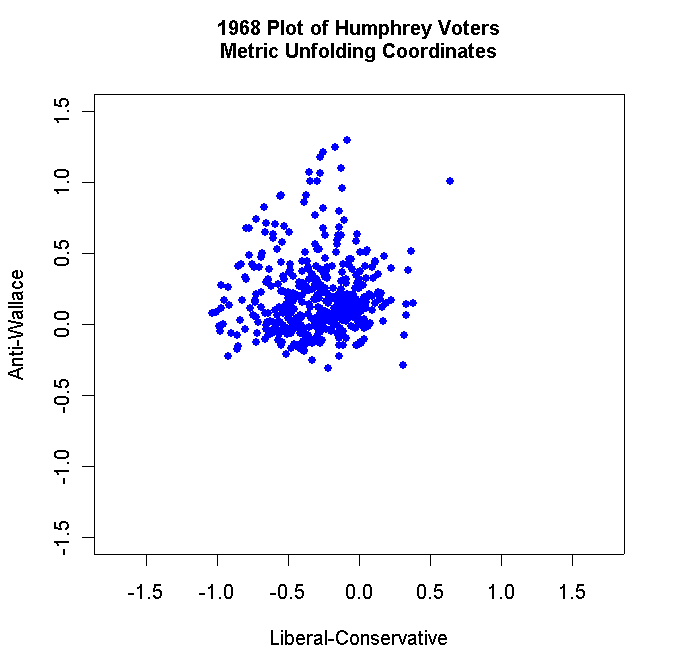
Label each plot appropriately and use solid dots to plot the respondents. Turn in all these plots.
Here are the first four lines of ELEC2000.DAT.
10787 4 8 0 0 0 2 49 1 0 65 60 30 40 70 50 998 998 40 59 75 63 65 6 1 3 6 4 0 2
21271 2 6 0 1 0 2 35 1 50 50 50 50 997 50 0 50 997 50 100 0 100 0 4 4 2 6 8 0 0
40285 2 6 0 0 0 2 63 0 70 55 55 60 65 55 55 65 50 60 70 65 65 90 6 5 5 5 5 0 1
50191 6 6 0 1 0 2 40 1 50 40 80 60 60 80 70 50 70 0 20 90 70 70 6 2 2 6 4 0 2
The variables, in order, are:
RESPONDENT ID = unique 8 digit number
PARTY ID = 0 to 6 -- 0 = Strong Democrat
1 = Weak Democrat
2 = Lean Democrat
3 = Independent
4 = Lean Republican
5 = Weak Republican
6 = Strong Republican
FAMILY INCOME = 1 to 22 - 1. A. NONE OR LESS THAN $4,999
2. B. $5,000-$9,999
3. C. $10,000-$14,999
4. D. $15,000-$24,999
5. E. $25,000-$34,999
6. F. $35,000-$49,999
7. G. $50,000-$64,999
8. H. $65,000-$74,999
9. J. $75,000-$84,999
10. K. $85,000-$94,999
11. M. $95,000-$104,999
12. N. $105,000-$114,999
13. P. $115,000-$124,999
14. Q. $125,000-$134,999
15. R. $135,000-$144,999
16. S. $145,000-$154,999
17. T. $155,000-$164,999
18. U. $165,000-$174,999
19. V. $175,000-$184,999
20. W. $185,000-$194,999
21. X. $195,000-$199,999
22. Y. $200,000 and over
RACE = 0 White, 1 Black
SEX = 0 Man, 1 Woman
SOUTH = 0 North, 1 South
EDUCATION = 1 High School or less, 2 Some College, 3 College
AGE = In Years
MARRIED = 0 Single, 1 Married
FEELING THERMOMETERS (0 TO 100)
= CLINTON
= GORE
= BUSH
= BUCHANAN
= NADER
= MCCAIN
= BRADLEY
= LIEBERMAN
= CHENEY
= HILLARY CLINTON
= DEMOCRATIC PARTY
= REPUBLICAN PARTY
= REFORM PARTY
= PARTIES IN GENERAL
LIBERAL-CONSERVATIVE SCALE (1=EXTREMELY LIBERAL, 2=LIBERAL, 3=SLIGHTLY LIBERAL,
4=MODERATE; MIDDLE OF THE ROAD, 5=SLIGHTLY CONSERVATIVE,
6=CONSERVATIVE, 7=EXTREMELY CONSERVATIVE)
= SELF-PLACEMENT
= CLINTON
= GORE
= BUSH
= BUCHANAN
PRE-POST INTERVIEW = 1 IF PRE-ELECTION INTERVIEW ONLY
VOTE CHOICE = 0 NON-VOTER
= 1 GORE
= 2 BUSH
= 3 3RD PARTY
MLSMU6 expects to read UNFOLD.CTL!! Consequently,
rename your current UNFOLD.CTL to UNFOLD_1968.CTL and then you can
copy UNFOLD_2000.CTL to UNFOLD.CTL.- Run MLSMU6. It will produce an output
file called FORT.22. The first 20 lines look
like this:
CLINTON -0.7879 -0.0317 153.1404 0.7198 1477.0000 GORE -0.7133 -0.1701 112.1776 0.7061 1468.0000 BUSH 0.8234 -0.2492 149.4325 0.5889 1458.0000 BUCHANAN 0.4576 1.0536 178.0645 0.3114 1246.0000 NADER -0.2737 0.7599 174.6307 0.2645 1094.0000 MCCAIN 0.2850 -0.6498 122.5794 0.3691 1182.0000 BRADLEY -0.0780 -0.7509 106.1498 0.3689 1088.0000 LIEBERMAN -0.3428 -0.6394 107.1314 0.4758 1096.0000 CHENEY 0.7002 -0.4687 107.9753 0.5099 1147.0000 HILLARY -0.8617 0.0625 203.7540 0.6459 1466.0000 DEMPARTY -0.6788 -0.1713 112.8208 0.6861 1453.0000 REPUBPARTY 0.8235 -0.3286 142.8395 0.5546 1447.0000 REFORMPTY 0.1644 1.0398 132.9094 0.3140 1128.0000 PARTIES 0.1949 -0.7946 158.0865 0.2290 1413.0000 1 0.3666 -0.0534 1.2943 0.3584 12.0000 2 -0.2740 0.6767 2.5447 0.5465 12.0000 4 0.0094 0.0645 0.8008 0.0000 14.0000 5 0.5073 -0.0010 1.3888 0.6249 14.0000 7 0.2719 0.0294 0.3600 0.5458 14.0000 8 -0.6582 -0.2931 1.8168 0.7683 14.0000 etc etc etc etc etc etcUse R to plot the 14 stimuli in two dimensions. This plot should be similar in format to the ones you did for the 1968 configuration above.
- Use Epsilon to insert the
VOTE CHOICE variable into FORT.22 (strip off the candidate
coordinates first). Turn in the Epsilon macro
you used to do the insertion and the first 20 lines of the file.
- Use R to make two-dimensional plots
of the Voters, Non-Voters, Gore Voters only, and
Bush Voters only. For example, your Gore Voter plot should look
something like this:
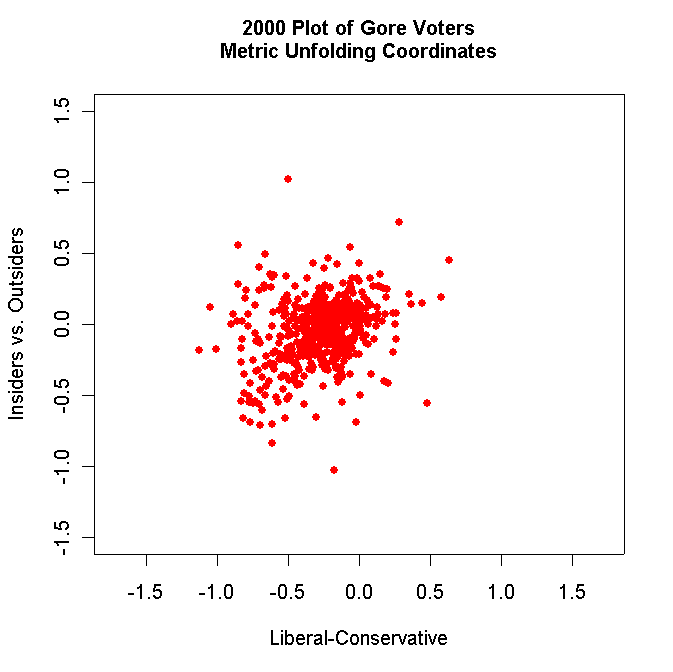
Label each plot appropriately and use solid dots to plot the respondents. Turn in all these plots.
- Use R to make smoothed histograms --
using the first dimension from the thermometer scaling --
of the Voters and Non-Voters only, and the Gore Voters, Bush Voters, and Non-Voters. For
example, your Bush-Gore-NonVoters plot should look
something like this:

Here is the trick for getting the percentage breakdown in the plot:# text(-1.0,0.53,paste("Gore Voters ", 100.0*round(goreShare, 3)),col="red",font=2) text(-1.0,0.5,paste("Bush Voters ", 100.0*round(bushShare, 3)),col="blue",font=2) text(-1.0,0.47,paste("Non Voters ", 100.0*round(nonShare, 3)),col="black",font=2) #Turn in the R code and the plots.