LEGACY CONTENT. If you are looking for Voteview.com, PLEASE CLICK HERE

This site is an archived version of Voteview.com archived from University of Georgia on May 23, 2017. This point-in-time capture includes all files publicly linked on Voteview.com at that time. We provide access to this content as a service to ensure that past users of Voteview.com have access to historical files. This content will remain online until at least January 1st, 2018. UCLA provides no warranty or guarantee of access to these files.

The Unidimensional Supreme Court

10 July 2003

In a recent piece in the Proceedings of the National Academy of Sciences Lawrence Sirovich analyzed the voting patterns of the current Supreme Court ("A Pattern Analysis of the Second Rehnquist U.S. Supreme Court." PNAS, 100 (24 June 2003):7432-7437). This piece received a great deal of publicity in the popular science press. The purpose of this short comment is to show that Sirovich's findings are consistent with current work on the Court by Political Scientists such as Bernard Grofman, Kevin Quinn and Andrew Martin, and Joshua Clinton, Simon Jackman, and Douglas Rivers.

This recent highly innovative research by Quinn and Martin and CJR in turn builds upon path-breaking work by Glendon Schubert (The Judicial Mind, 1965, Evanston: Northwestern University Press), David Rohde and Harold Spaeth (Supreme Court Decision Making, 1976, San Francisco: W. H. Freeman), Jeffrey Segal and Harold Spaeth (The Supreme Court and the Attitudinal Model, 1993, Cambridge: Cambridge University Press), Lee Epstein and Jack Knight (The Choices Justices Make, 1998, Washington, DC: CQ Press), Bernard Grofman and Timothy Brazill ("Identifying the Median Justice on the Supreme Court Through Multidimensional Scaling: Analysis of 'Natural Courts' 1953-1991." Public Choice, 112:55-79, 2002), to name just a few. An excellent summary of the literature can be found in "The Dimensions of Supreme Court Decision Making: Again Revisiting The Judicial Mind" by Kevin Quinn and Andrew Martin.

Sirovich's approach was to perform Singular Value Decomposition (SVD) on the matrix of Supreme Court "roll calls" -- 468 votes cast during the 8 year period 1995-2002. In multidimensional scaling work the normal practice is to discard the unanimous votes because they contain no information about the ideal points of the voters unless strong assumptions are made about the proposal process. Sirovich included the 220 unanimous votes in his analysis. Consequently, when he performed a SVD on the 9 by 468 matrix the first singular vector was, in effect, (1/3, 1/3, 1/3, 1/3, 1/3, 1/3, 1/3, 1/3, 1/3) -- that is, the first singular vector picked up a "unanimous" dimension with all the justices almost at the same point (see Table 3, p. 7434). His second singular vector was: 

Stevens    -0.445911 
Ginsburg   -0.367567 
Breyer     -0.327401  
Souter     -0.3127 
O'Connor    0.104212 
Kennedy     0.174192 
Rehnquist   0.304502  
Scalia      0.403145  
Thomas      0.405752
This is clearly a liberal-conservative dimension that closely matches the standard journalistic description of the Court.

In Table 2 Sirovich shows the Joint Probability for Disagreement for the Court. This table is reproduced below:

Breyer       0.00000  0.11966  0.25000  0.20940  0.29915  0.35256  0.11752  0.16239  0.35897
Ginsburg     0.11966  0.00000  0.26790  0.25214  0.30769  0.36966  0.09615  0.14530  0.36752
Kennedy      0.25000  0.26709  0.00000  0.15598  0.12179  0.18803  0.24786  0.32692  0.17735
OConnor      0.20940  0.25214  0.15598  0.00000  0.16239  0.20726  0.22009  0.32906  0.20513
Rehnquist    0.29915  0.30769  0.12179  0.16239  0.00000  0.14316  0.29274  0.40171  0.13675
Scalia       0.35256  0.36966  0.18803  0.20726  0.14316  0.00000  0.33761  0.43803  0.06624
Souter       0.11752  0.09615  0.24790  0.22009  0.29274  0.33761  0.00000  0.16880  0.33120
Stevens      0.16239  0.14530  0.32692  0.32906  0.40171  0.43803  0.16880  0.00000  0.43590
Thomas       0.35897  0.36752  0.17735  0.20513  0.13675  0.06624  0.33120  0.43590  0.00000
Note that this table does not exactly match Sirovich's Table 2 in that his table has rounding errors. For example, the disagreement probability of the pair (O'Connor, Kennedy) is shown as 0.156 and the disagreement probability of the pair (Kennedy, O'Connor) is shown as 0.15598. These discrepancies are only at the 4th or 5th decimal place (the R software often produces this type of discrepancy!) so I simply chose one of the values to make the matrix symmetric. This should have absolutely no effect upon my analysis below.

The above matrix is known in Psychometrics as a dissimilarity matrix and the properties of this type of data have been studied for almost 100 years (see The Past and Future of Ideal Point Estimation for an overview). Dissimilarities data can be treated as squared Euclidean distances and double-centered. This operation removes the squared terms and leaves only the cross-product matrix. This matrix is symmetric and can subjected to standard eigenvalue-eigenvector decomposition. A Skree plot of the eigenvalues is a good method of determining the dimensionality of a voting matrix (although it should never be used as the only method -- it should always be used in conjunction with standard fit statistics produced by a spatial voting model!). Below is a graph of the eigenvalues of the double-centered disagreement matrix:



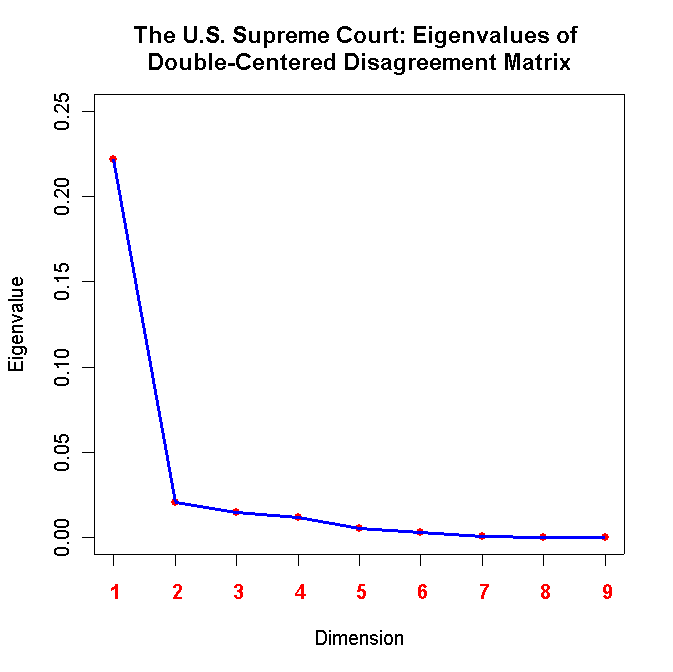
This pattern strongly suggests that there is only one dimension underlying the matrix. Indeed, below is the first eigenvector: 

Stevens    -0.4981644 
Ginsburg   -0.3376050 
Breyer     -0.2985069  
Souter     -0.2694862 
O'Connor    0.1074960 
Kennedy     0.1602323 
Rehnquist   0.3024991 
Scalia      0.4167577 
Thomas      0.4167775
this ordering exactly matches the 2nd singular vector shown above.

Further evidence of unidimensionality comes from a non-metric multidimensional scaling analysis using KYST. Below is the one dimensional configuration from KYST: 

Stevens      -1.248
Ginsburg     -1.100
Breyer       -1.054
Souter       -1.041
O'Connor      0.700
Kennedy       0.776
Rehnquist     0.899
Scalia        1.034
Thomas        1.034
This ordering matches the two above. The STRESS value was 0.0098 indicating nearly perfect unidimensionality. Below is the Shepard Diagram for the scaling:



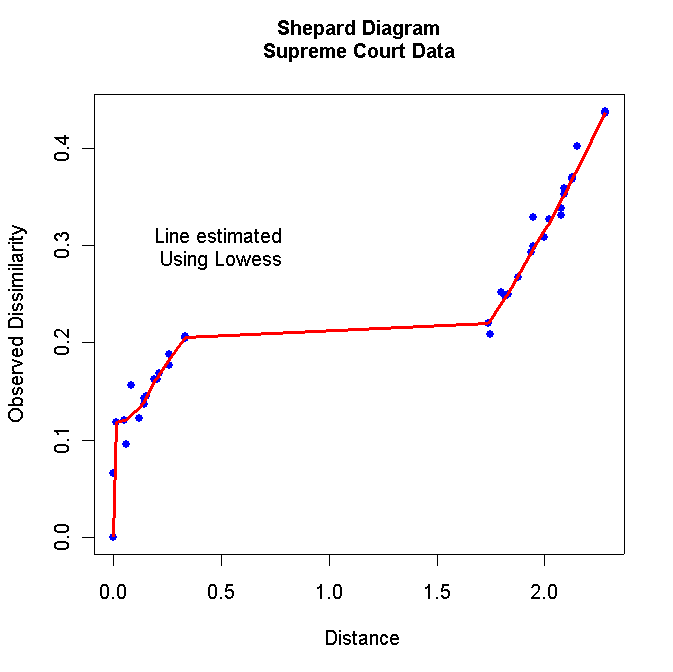
Further evidence of unidimensionality of the current Court is provided by an application of Optimal Classification Analysis (OC) to the voting data for the current Court through 2001. In one dimension OC produces a rank ordering and in two or more dimensions is provides point estimates (these are really polytopes -- for a detailed explanation see): The total number of non-unanimous votes was 293 (the total number of votes in the sample was 512) and in one dimension the correct classification was 93.1% with an APRE of .755. OC produces the following rank ordering:

    1 STEVENS        23  291   0.921   1.000
    2 BREYER         30  290   0.897   2.000
    3 GINSBURG       18  291   0.938   3.000
    4 SOUTER         19  293   0.935   4.000
    5 KENNEDY        13  293   0.956   5.000
    6 OCONNOR        29  290   0.900   6.000
    7 REHNQUIS       20  292   0.932   7.000
    8 SCALIA         13  292   0.955   8.000
    9 THOMAS         16  292   0.945   9.000
In the ordering above, the number just to the right of the Justice's name is the classification error and the number to the right of that is the total number of votes cast by the member. For example, placing Justice Stevens at rank 1 resulted in 23 classification errors out of a total of 291 votes cast. The proportion correct is 218/222 = .921 (which is shown just to the left of the rank).

The rank-ordering from OC reverses the positions of Kennedy and O'Connor and Breyer and Ginsburg compared with the configurations above.

In two dimensions the correct classification was 97.0% with an APRE of .893. Below is a plot of the two dimensional OC configuration (Justices in Blue are Republican appointees and Justices in Red are Democratic appointees):



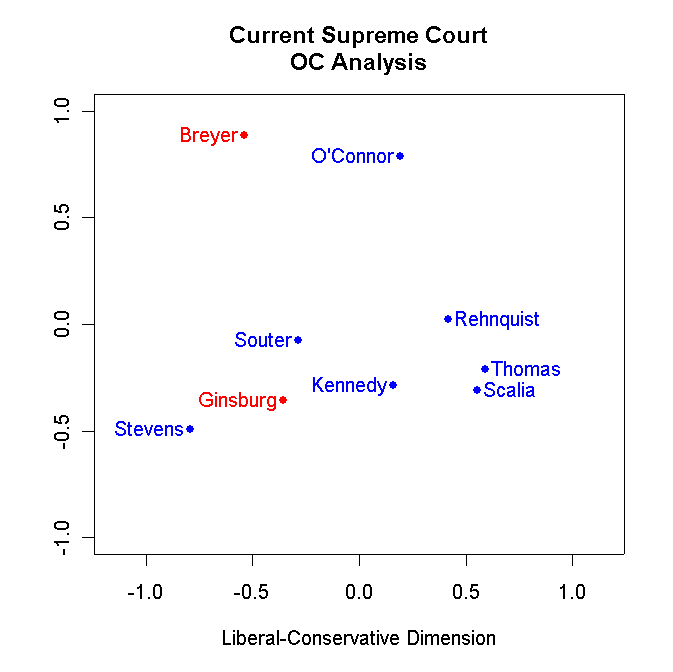
The OC results suggest the possible presence of a weak second dimension. However, this is probably simply noise fitting. Note that the second dimension is simply a Breyer-O'Connor dimension. Breyer and O'Connor are the two worst fitting (89.7% and 90.0% respectively) justices in one dimension. In two dimensions the fits for Breyer and O'Connor jump to 99.0% and 98.6% respectively whereas the increases in fit for the other justices only increase from 1 to 4 percentage points.

The bottom line is that the current Court is basically unidimensional.

Again, for a thorough in-depth analysis of the Supreme Court over the 1937 to 2000 period see the innovative markov-chain monte-carlo (MCMC) work of Kevin Quinn and Andrew Martin. The 1953-1991 period is analyzed by Bernard Grofman and Timothy Brazill who find basic unidimensional voting, and the 1994-97 period is used by Joshua Clinton, Simon Jackman, and Douglas Rivers to illustrate their IDEAL program in an one dimensional analysis.

Site Links

VOTEVIEW Blog
NOMINATE Data, Roll Call Data, and Software
Course Web Pages: University of Georgia (2010 - )
Course Web Pages: UC San Diego (2004 - 2010)
University of San Diego Law School (2005)
Course Web Pages: University of Houston (2000 - 2005)
Course Web Pages: Carnegie-Mellon University (1997 - 2000)
Analyzing Spatial Models of Choice and Judgment with R
Spatial Models of Parliamentary Voting
Recent Working Papers
Analyses of Recent Politics
About This Website
K7MOA Log Books: 1960 - 2017
Bio of Keith T. Poole
Related Links